Anthony Repetto/Concept Log

Concept Summaries

last updated: 20. July, 2011

Here are a few concepts OSE may find useful. I'll continue to update, and link to detailed sub-pages as I draft them. This page is the reference point for work I find interesting; each topic has a summary of its design features, and the issues it addresses. I'd love to develop simple visualizations for these ideas, and others; text is limited.

Project-Specific Considerations

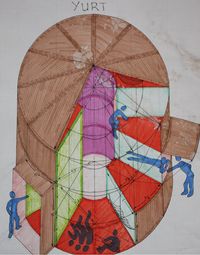
Yurt

Yurt Sketch, with rough measurements

The intention is to provide a quick start-up dwelling for new GVCS sites; same-day housing, while you wait for the CEB machine to bash bricks.

For disaster relief, slums and outliers in the developing world, and migrant/start-up labor sites: a simple, sturdy tent structure, encircling rings of 'cubbies', layered like a cake. (Picture a stack of pineapple rings.) Rough tent dimensions: 20' (6m) wide, 12' (3 2/3m) high walls, 15' (4 1/2m) apex.

The interior cubby rings are broken into 12 radial segments; one segment is the entry way, 11 are private tents. The center is open, 6' (1 4/5m) wide, with laddering on the frame to ascend into third-tier cubbies, or to access 'attic' storage. Each cubby is 4' (1 1/5m) tall, 1 1/2' (1/2m) wide at its interior entry, 7' (2 1/6m) long, and 5 1/4' (1 3/5m) wide along the exterior wall. Materials are: steel framing (for 34 people, plus personal supplies, or up to 100 people as a disaster shelter; mother, father, & small child per cubby - over 20,000lb (10 tonne) support necessary); exterior skirt (a single weather-resistant sheet, lying over the frame); and individual cubby tents (edges threaded with support chords, which attach to frame - at least 600lb (270kg) support necessary).

When taken apart, its compact form can be stacked in a 20' (6m) wide cylinder, which could double as a water tower, silo, or fuel tank, and, if 15' (4 1/2m) tall, the canister could hold as many as 10 such yurts. (Immediate shelter for up to 1,000 people, or 340 folks as private dwellings.) Include tools, emergency supplies, etc. for a village-in-a-box.

Trencher

There are already a wide variety of earth moving machines. Bucket wheels work quickly, but they're huge, expensive, and require expertise. Scrapers remove loose top soil, but have to haul their loads away, reducing their time-use efficiency. I wouldn't bother with an excavator. If we could build a smaller LifeTrac attachment, irrigation canals would be within reach. The primary limitations to existing designs are fuel and capital efficiency. Considering the optimal case, where you only account for the work of separating and lifting the soil, a gallon of gasoline should be able to dig a huge canal. But, existing machines breeze through fuel, and have either unacceptable lag times, requiring more operator hours, or huge up-front and maintenance costs.

I was honestly wondering, at first, if it would be more fuel and time effective to drill blast holes for ANFO, and clean up the canal faces afterwards. (At least it would be fun!) But, there might be an easier way: keep the bucket wheel's conveyor, for continuous operation, and switch the wheel out for a row of 'jackhammer' shovel teeth, which punch down into the leading face of the canal, and fold the soil onto the conveyor. The shovel face's dig cycle is shown in the sketch. (soon!) Depending upon the way it was attached to the LifeTrac, the jackhammer force on the soil surface could be driven by compressing and releasing the attachment angle; the rear wheel of the LifeTrac hoists up, transferring weight to the support wheels behind the trencher attachment, and when the hydraulics are released, the frame presses the shovel faces into the soil. (more sketches soon)

This is a new kind of earth-mover, so it violates a few OSE specifications - namely, legacy design. But, if the legacy designs are insufficient for our uses, why not make new ones? I'm not about to patent this; I'd love for Sudanese farmers to have it, to dig canals along the Sudd. Heck, if it's fuel-efficient enough, the Indian Subcontinent would go nuts for it. I'll need to get more specifics, to lay out strains and flow rates. Updates shall continue!

Chinampas & Terra Preta

We don't all live in the tropics. But a lot of us do, and in hot climates, the most efficient farming method is widely spaced canals and long, large raised beds with a complimentary mix of crops. The Aztec and later inhabitants of the Valley of Mexico used these swampy gardens to grow maize, squash, beans, and chili, at an estimated input cost of 1 calorie per 120 calories of foodstuffs produced. These chinampas (and Beni camellones, as well as Javanese, Egyptian, Bengali, and Chinese terrace and canal systems) are ideal for combining utilities and recycling wastes through multiple high-value cultures: trees are grown along the waterline, to support the soil bed, aid in filtration and water dispersion through the soil, and provide timber and craft materials; canals are efficient transport routes, reservoirs, and climate control; they grow wet grasses for feed and fertilizer, and can support very productive aquaculture; dense, mixed vegetable plots meet diverse nutritional needs, harvesting 3-4 times a year without fallows, and marginal vegetation supports livestock productivity.

In more arid climates, canals require prohibitive labor costs to set up, and water use is limited. The trencher (hopefully) makes it easier to afford canal-digging, but what about evaporation? I propose covering the canals with clear plastic sheets, propped up on A-frames running the length of the canal zones. With interior 'sluices' and 'reservoirs' along the hem-line of the sheets, condensation is gathered for personal use as purified water. During the day, sunlight heats the water and fills the A-frames with steam. The coolest air is pushed out, under the sides of the canal sheet, along the raised beds. Remaining humidity, cooling in the evening, condenses in the distillation reservoirs. Throughout the day, the condensing humidity that is pushed out from under the sheet completes its condensation in the air just above the raised beds: a thin layer of fog would be visible for most of the morning, providing 'drip' irrigation and protecting crops from wilting heat.

The last piece of the puzzle is soil management: water flow through the soil beds leeches soluble organic nutrients, and chinampa maintenance mostly involves dredging the canal bed for silts and grasses, to re-mineralize the soil. The Beni people of Bolivia and western Brazil solved this problem thousands of years ago. (That qualifies as a legacy technology, right?) Here is how they did it: composted refuse, detritus, and manure ('humanure', too) were allowed to 'stew' in a pit. Fragmented bio-char was added, (I recommend a syngas gasifier to get your char) to bind with bio-active nutrients in the slurry. They'd give it a few days to soak, so the char wouldn't be a nutrient sponge when they added it to the ground. Then, pot sherds were mixed in, until it had a good consistency. The nutrients stuck to the char, and the char painted the ceramic fragments: because pot sherds don't wash away, neither does your plant food. Folks in Brazil call this anthropogenic soil 'Terra Preta do Indio' - 'Indian Black Earth'.

Bio-char is a very porous material - that's what lets it absorb and bind to so many things. And ceramic fragments aren't slouches when it comes to surface area, either. Combined, they provide a huge, pocked surface for microbes and mycelium, they prevent soil compaction and run-off, and are great anchors for root structures. Australian field experiments have shown that, with 10 tonnes of char per hectare (that's 1kg bio-char per 1sq. meter, or almost 5sq.ft. per pound of char), field biomass triples, and NOx off-gassing is cut to 1/5th of pre-char levels. Once terra preta is mixed into surface soils, the microbial cultures will continue to spread downward, extending the zone of fertile soil at a rate of ~1cm/yr. In the many native deposits across the Amazon, locals will mine the soil at regular intervals, scooping up surface cultures for home gardens, and returning years later to find that more of it has grown into the ground. Even with heavy Amazonian rains and floods, these patches have remained fertile without maintenance (and still spread!) since they were created, as long as 3,000 years ago.

So, dig canals with the trencher, cover them with distillation tents, plant complimentary crops, and recycle 'wastes' into terra preta. I'll keep updating with data on input/output rates and estimates of productivity and costs. More diagrams, too.

Insect Farm Module

Especially during the initial phase of GVCS development, local resources are relatively scarce and underdeveloped. The biggest hurdle to new endeavors isn't the level of return on investment - it's the return's velocity. If a farmer has to wait a year, or even a season, before they can feed themselves locally, the choice may be beyond their means. Insects farming is a quick, low-budget way to convert underutilized and abundant resources into fast food, feed, and fertilizer.

Given a local mix of scrap timber, fibrous vegetation, and rotting organic matter, then termite, worm, and black soldier fly 'bug bins' are proven ways to quickly turn inedibles into high protein, fatty, and mineral-rich foods. A goat will do it, too; but only for fresher roughage. Ruminant digestion is very efficient for producing milk, which can be processed and preserved as goods with higher value than bugs, but it's a temperamental gut. So, give the fresh stuff to a goat, and all the junk to the bugs.

There are plenty of OS designs for worm bins, and more soldier fly bin designs are popping up all the time. I'd love to see some good termite set-ups. If we could turn these into modules, for linear attachment and easy swapping/repair, I think we've got a good temperate-climate bug kit. Jungles are different.

There are a lot of bugs in the tropics. This means, anything you look at has a bug that will eat it. Huge potential for composting schemes, right? But they're mostly species-specific consumers. And a lot of those plants are toxic to everyone else. So, instead of trying to contain all those bugs, there's more value in creating a good climate for them around you, and investing in bug-eaters. What that looks like varies, from tropic to tropic. Folks'd have to figure it out. I'm for bats and ground fowl, mostly. :)

Mini-Steamer

Large steam engines require strong materials and a good bit of work. Sterling engines operate on smaller temperature gradients, at higher efficiencies (due to heat regeneration which preserves temperature gradients within the pump), but can't manage higher power applications. (Sterling engines can only handle a limited flow rate, because of low rates of heat transfer through the walls.) The goal is a small, mid-power steam engine, with a minimalist design that operates at low pressure, and 'preserves' temperature gradients, for Sterling-like efficiency. Primary use is for pairing with the Fresnel Solar modules. Ideally, the engine would induce current directly, selling back to the grid, or storing power in a battery/capacitor over the course of the day.

My guess is, we could make a doughnut shaped 'piston chamber' with rotating magnetic paddles, wrapped inside a solenoid. (See rough sketch. ...soon) The steam/hot gas enters the radial cavity between two paddles, causing expansion as well as rotation in one direction (the design sketch shows how paddles are linked to each other by their orbiting rings, so that expansion force drives rotation). As the paddle orbits the ring, paddles on the other side press exhaust gas through a second valve. Because the steam enters one side of the ring, and exits after making an almost complete loop, heat transfer to piston walls follows a gradient around the ring. (Traditional steam engine piston chambers alternate between hot and cold, so each new burst of steam must warm its container, as well as expand.) As the steam speeds the orbits of the paddles, their moving magnetic fields induce current in the solenoid. Paddles could move with minimal impedance, for low-pressure steam, or the solenoid resistance could be stepped up, to extract more energy from hotter steam. Stacking modules, and routing exhaust from one into the module above it, would step-down steam temperatures and pressures; the ability to operate with lower pressures would be key for raising total efficiency. Combined Heat & Power (CHP) set-ups could tailor their capital use on the fly, depending upon how much heat was being wasted, simply by adding or removing mini-steamers from their step-down train.

With a ring of orbiting paddles, in-flows are separated from exhaust by multiple seals, reducing the risk of leaks & back-flow, and eliminating the need for troublesome bump valves. Consider, as well, that steam is transferred through a loop, with only the solenoid to impede it: excessive pressure is vented in a single orbit, by a natural increase in paddle speed. No risk of explosive pressures from compression strokes! Also, notice that the lever arm of a traditional steam engine's crank shaft is best at the beginning of the piston stroke, and transfers much less force per arc length as its rotation peaks. (Especially because the force of the piston is greatest at the start, and tapers as expansion completes.) This jerk requires an over-engineered crank shaft! (No, not 'some butt-head in the corner talking about standards' jerk; jerk is change in acceleration over time.) In fact, the solenoid mini-steamer wouldn't even have a crank shaft. DC, baby. :)

I've been contemplating solenoid production: Japanese yosegi (wood mosaics) are my inspiration. (More diagrams coming soon!) On the outside of a roller drum, bend sheets of copper into a spiral, pouring insulating epoxy (or similar material) between the layers just before the roller squeezes them together. Once the ring of conductive/insulating layers has solidified, plane layers off of the flat faces of the ring, to create sheets with pinstripes of copper and insulation. Curling these onto themselves, and bonding the copper, forms a single solenoid coil. Layer these coils, with more epoxy between, to create a nested 'Russian Doll' of many simple solenoids. And, with the equipment for such a technique, how cheap would it be to switch production to capacitors?

At-Work - I was sketching out the flow of pressures in the chamber, and getting rotation to start and stick is a bit trickier than I expected! :) Interesting options, tangents, concepts bubbling up. I'll start the mini-steamer page, to go into discussion of feasibility and limits to maximum power. Each variation I'm looking at has its own kinks, but there might be a good mix between them, or a new direction. Otherwise, I'm happy to toss it in the 'maybe later' or 'not at all' piles.

Design Update - Found it! :) I was over-engineering the paddles. They can float freely, four or more paddles riding in a loop, like red blood cells through alveolar ducts. Interesting note: running current into this set-up will cause the paddles to PUMP in reverse... like Motor/Generators and Sterling/Refrigeration, you could use this to get current from pressurized fluids, or pressurize fluids using a current! Looking over the design constraints, you could also scale it down quite a bit... watch-sized pressure pumps, to grab that little bit of heat from your tea pot? Diagrams shortly...

Organization & Impact Considerations

Allocation

"Taylorism for Lovers"

External Considerations

On Good Will

We like to pretend that people are gullible, guilty, afraid, exhausted, distracted, obsessed, and selfish. These things happen to all of us, but they don't constitute human being; they're not what we ARE. The majority of most peoples' days are warm, understanding, generous, forgiving, and hopeful. Think about it: what percent of your day did you spend in despair, rage, or regret? The illustration I remember is: if two of us turn the same corner, and bump, most of the time we'll be surprised, apologetic, and full of care. Catch us off-guard, and we show you our true selves: we like people, and hope they like us. I think people are awesome; life is a mysterious and fantastic creation, and humans happen to be the most mysterious and fantastic part of it. Humans are worth more than their weight in gold, or flowers.

Our super-cool-ness isn't because we can DO what other creatures can't; it comes from the KINDS of choices we make, given what we CAN do. I love my kittens, but if they were bigger than me, they'd eat me. I happen to be bigger, and I don't eat them. What's going on? It's that 'love' thing. We feel existence is delicious, and whenever a sour spot hits us, we get the crazy itch to make it sweet, if only for OTHERS. OSE is a living demonstration of this: we toss our hours in, hoping others will find sweetness.

I'd single out patent law as the prime example for understanding the death of our faith in good will. An inventor creates something new, but needs cash for capital, to realize his creation. Patent law gives him a temporary monopoly, so that guaranteed profits will lure investment to the inventor, instead of the first savvy industrialist who copies him. Edison famously corrupted this system, and corporations run on his model of corporate licensing. What you invent on the job, is owned by the company that employs you. Those savvy industrialists don't bother to copy anymore; they write contract. The inventor's idea will (occasionally) enter the market, but he doesn't usually profit. (A 'bonus' isn't a share of profit; ask guys at Bell Labs.) Meanwhile, the pablum fed as justification for corporate ownership of human thoughts is "without patent, inventors wouldn't have an incentive to invent," as if starving or money-mad people are the only ones who bother to create. Suppose I have all my needs covered; will I stop creating, or create more? Evidence from behavior studies validate Erickson's hierarchy of needs - once your bases are covered, you start working on creative fulfillment and community.

And, those higher drives can push you into actions necessary for your goals that threaten your lower needs: Gandhi fasted to save India. Our behavior, working toward these higher goals, is often called 'revolutionary' - we see the value of our choices as greater than the value of conformity and continuity. Our choices are purposeful and specific, but they are free to be so because we start by opening ourselves to possibilities outside the norm. So, I wouldn't say that 'necessity is the mother of invention' - for me, necessity is the mother of conformity, and blatant disregard is the mother of invention.

Our most valuable disregard is of failure. We'll keep trying again, because some things don't work until the 1,001st attempt. We learn from the experience, but we don't learn to give up. This generosity and perseverance is innate, and we can build plans around it. How? Stanley Milgram pioneered work on this: his best guess is that you only need to nudge folks' situations. Our habits and choices vary, from person to person, but the variation in each of our total behaviors is small. We all grow up, have friends, work on stuff, etc. Where does our behavior's diversity appear? The situation decides. If you're in a theater, you're probably sitting quietly, facing forward. Your behavior isn't predicted by your past, genetics, or mind set; it's the location and event that guide us. If we create situations where folks are challenged AND empowered, that dogged selflessness wells up in them. Let's get rid of patent, and the other protectionist crutches. I'll be outlining alternatives on the detailed sub-page.

Theory & Hypothesis

Binary Search

We have lots of ways to search for and sort the information we need. Google's search algorithm made Brin & Page rich, and made our lives simpler. Recognition algorithms, for voice, image, text, weather, network routing, and protein folding, are pretty useful, too. These are also the tools you'd need to optimize allocation of time and resources, assuming a single agent. (Yeah, it's not a market assumption, but it applies to OSE, and that GVCS game I heard mentioned.) Search is a powerful modern tool, and it'd be great to have an Open Source Search Algorithm. I've got one: it's an extension of Binary Search (cut the search in half, with each test) into high-dimension spaces. (There are elaborations into combinatorial spaces, too, but that's a worm-can factory...) I'll outline the theoretical direction, then the software format. Examination of the search technique's flow shows some interesting new things, deep inside mathematics. I'll get into that theory bit by bit.

Simple Binary Search

"I've picked a number between 0 and 100. Try to find it, in the fewest guesses possible. I'll tell you, after each guess, if you're 'too high' or 'too low'." The best strategy for this game is to divide the space in half - pick '50', first. If I say 'too high' OR 'too low', you've eliminated half the space from consideration. Wow! Your next pick is either '25' or '75', and on... How does this get applied to high-dimensional protein folding problems? First, instead of 'guessing right' or 'guessing wrong' (a '1' or '0'), we have to allow the whole range of success. ('good', 'better', 'best'... the 'highest peak of a fitness landscape', an 'optimum') Also, no one hands us a 'too high'/'too low' response - we'll have to figure that out using statistics gathered from the history of our guesses. What's the most efficient use of that historical data, to inform the most appropriate method of guessing?

Existing Methods

Let's look at some existing methods - hill-climbing, genetic algorithms, and Gaussian addition. That'll give us a good idea of where we can improve. The general format used to talk about them is a 'fitness landscape'. For example, I want to know how much sugar and cocoa powder to add, to 8oz. of milk, for the tastiest hot cocoa. Sugar (grams) and Cocoa Powder (grams) are the two feature dimensions, and Tastiness (user feedback scale) is the fitness dimension. Like a chess board, each point on the ground is a different set of sugar and cocoa powder coordinates. Those points each have a different Tastiness, represented by the landscape's height at that point. The unknown hills and valleys of this landscape are our search space - we want to check the fewest points on the chess board, and still find the tastiest hot cocoa. It's like playing Battleship.

Hill-climbing tries to do this, by checking a random point, and a point close to it. If the point close by is lower than the first one, you pick a new point nearby. The first time you get a new point higher than the old one, you know 'a hill is in that direction' - move to that new point, and start testing randomly near it, until you find the next step upwards. Eventually, you'll climb to the top of the hill. But, is that the highest of the hills? Once you're at the top, jump to some other random point, and climb THAT hill, too. Hopefully, you'll eventually land on the slopes of the highest hill, and climb to its peak. The only history you keep track of is the old point (your current 'position') and the new point that you're now considering. Hill-climbing happily lands on many sides of the same hill, climbing to the same peak, without thinking ahead. With little memory of its history, random guessing and point-to-point comparisons are all it can manage. This is all you need, for low-dimension searches. (sugar & cocoa is a 2-D feature space... what if there are 200 features?) Higher dimensions pose a problem. First, a few made-up words: if you have a hill, let's call the area of feature space under it, 'the footprint'. And, the lower half of the hill, all the way around it, is 'base camp'. The upper half of the hill is 'the ridge line'. For a hill in one feature dimension, (it'd be a line peaking, /\) the footprint of the base camp is about twice the size of the ridge line's footprint. In two dimensions, the hill looks like a pyramid, and the base camp's footprint is 3/4ths of the total, while the ridge line's is the remaining 1/4th. For n-dimension feature spaces, the ridge line footprint shrinks quickly, as 1/(2^n) of the total. In 200 dimensions, that's 1/(2^200), or about 1 trillion-trillion-trillion-trillion-trillionth of the total footprint. It's very likely that a hill-climber will land on a high peak's base camp, but in high-dimension spaces, there's NO chance of hopping from there onto the ridge line. Hill-climbing will land on a hill, and hop randomly in different directions, but none of those hops will get it further up the hill. It stalls, hopping in circles around base camp, and says 'this is a peak'.

Genetic algorithms aren't good for finding new peaks. You throw down a shotgun splatter of random coordinates, and see which ones are higher up on the landscape. Swap coordinates between the highest of them, and kill off the low-landers. Things'll evolve, right? Nope - if your initial winners were at coordinates (a,b) and (c,d), their offspring will land on (a,d) & (c,b). But, if (a,b) is on a different hill than (c,d), those offspring will probably be landing in valleys. And the parents have no way of learning from their mistake! (interesting tangent - what if the parents lived and died by the measure of their offspring's fitness, instead of their own? or bred preferentially, based on the fitness of their pairings?) Two parents, high on opposite hills, would keep insisting on having low-lander babies, wasting valuable computer time, re-checking the same dumb coordinates. However, if the whole population is hanging out on the same hill, then, even if that hill is moving and warping, the population will drift along with it, staying on the crest like a surfer. That's all genetic algorithms can do well. And, considering how small a ridge line's footprint can be, there's no reason to believe genetic algorithms would work better in high dimensions. No memory of history, doomed to repeat the mistakes of their forefathers.

Gaussian addition starts to look like a method with memory of its past: every time you test a point in the space, lay down a normal curve ('Gaussian' is the math-name for the statistical bell curve) at that place. This is a good idea, when you're estimating something like local levels of ground minerals, because it's unlikely that those minerals are everywhere. Undiscovered deposits are likely near known concentrations, and nowhere else; we use Gaussians for surveying. But, are those assumptions accurate or useful for other kinds of landscapes? (A softly undulating surface, with many local peaks of slightly different heights, for example?) Nope, they are biased toward underestimation. Do they at least make best use of their history? No luck, there. A normal curve isn't a neutral assumption: you are assuming equal variation in each dimension, with hills and valleys having the same average slope, whichever way you look. Real optimization problems have to address the fact that you don't know each dimension's relative scale ahead of time. One dimension may hop between peaks and valleys as you change its value from 1->2, 2->3, etc. while another is a slow incline stretching across the values 0->1,000. A Gaussian would predict, based on a test point, that a gentle normal curve extended in all directions EQUALLY. It assumes equal variation in each dimension, without a way to test this assumption. Darn.

Binary Search

Let's look at my alternative. As you test points on the surface, and find their fitness, link them together to form a 'polygon mesh' - connect near-by points with straight lines, forming a rough-hewn surface of triangles, like an old '3D' video game. Variation between those points is equally likely to be up, or down, so the straight line is the best guess of the unknown, intermediate points' fitness. And, the farther you get from a tested point, the less certain you can be of other points' fitness. (This smooth drop in certainty is the 'correlation assumption' that all search relies upon: if two points are close to one another, they are more likely to have similar fitness to each other, than the space as a whole. The only spaces that fail to behave this way are noisy or fractal. We're not trying to search them, anyway, so this is fine.) That means, the greatest variation from the polygon mesh is likely to be at the center of those polygons, farthest from all the tested points. Also, as the diagram shows, (soon!) hopping from center to center this way is the faster way to leap toward peaks. Much like our intuition, the software expects the peak to be 'somewhere between those higher spots'. This is getting a bit wordy, so I'll be posting lots of diagrams. They'll do a much better job; bear with me for now?

So, imagine that chessboard of sugar and cocoa powder coordinates, with a few fitness points hovering above it. Connecting them to their nearest neighbors, to form the polygon mesh, already gives you a vague idea of the fitness landscape's total shape. This is unlike hill-climbing and genetic algorithms; they spit out the coordinates of the best results they've found, but don't bother to give you a holistic view. Their lack of vision stunts deeper analysis of the space, and lets us pretend that we've searched more thoroughly than we have. ("Oh, there's a huge gap in our testing, in this corner..." "Huh, the whole space undulates with a regular period, like a sine wave..." "That hill-climber was just approaching the same peak from 100 different sides..." These are insights you can't get with existing methods.) To save on run-time and coding, you don't have to visualize the space in my version, but the data set lets you do this at any time, if you'd like. That's nice! :) Now, knowing that variation is greatest at polygon centers, how many centers are there? On a two-dimensional chess board, each polygon is made of three points (sometimes four, if they form a rhombus-like shape); and testing the center of a polygon breaks it into three new polygons. Like a hydra, each new test adds a number of new centers equal to the dimension+1. So, after testing 200 points on a chess board, you could expect almost 600 centers. Here's the important insight: because the centers are the points of greatest variation, they are the only places you have to consider checking for peaks. You get to ignore the rest of the space! (This is a great way to 'trim the search'.) Now, we have to choose which centers to test first...

Suppose you've already tested a few points, naively. (I'll get into the best starting positions later; that's when you'll see how this is a form of Binary Search.) You have their polygon mesh, and you've found the centers of those polygons. Which one is most likely to produce a peak? You get a better answer to this question, the more you develop a statistic of the data history. Consider: when you test a polygon center, the plane of the polygon is the best naive estimate of the center's fitness. Once you check with reality, (or computer model) and return that point's fitness, it probably won't be exactly the same as the polygon's prediction. Keep a log of these variances. (Variation, explicitly, is deviation from the plane, divided by distance from the nearest polygon corner.) They are your statistic. As you refine this statistic of variance, you'll have a better guess of how much higher fitness that center could be, and what probability it has of being each height. You're only trying to test centers that will give you a new peak, so you only need to compare the variance to the height of the fittest point you've found so far (I call it 'the high-water mark'). For each center, what is the probability that it will contain a new, higher peak? (The portion of variance above the high-water mark.) And, what is the average gain in height, if it were to be a new, higher peak? (The frequency-weighted mean of the portion of variance above the high-water mark.) Multiplying the probability of an event, by the gain if it were to occur, is your pay-off or 'yield'. (If I have a 10% chance of winning $1,000, that's an average yield of 0.10($1,000)=$100.) Using the variance ogive (I avoid normal curves like the plague... I'll go into why, later) and the high-water mark, you can calculate each center's expected yield. List all these centers' coordinates and yields, sort by highest yield, and test the first center on the list. As you test each of these centers, they, hydra-like, create n+1 new polygons (for an n-dimension feature space), adding n+1 new centers to your list. Re-sort, and pick the highest-yield center. Repeat until you're satisfied. :) That's basically it.

Details

But! There are a few important additions. First: Gaussian addition assumed equal variance in all dimensions, and we wanted to avoid the same mistake. As you accumulate tested points, make a list of the vectors between them (those polygon edges). We're going to find the 'normalizing vector' - the stretching and squeezing of each dimension, that you need to make average slope the same in all directions. We don't need a perfect estimate; it'll keep being refined with each new center tested. We just want to use a method that avoids bias. (It won't start drifting toward extremes; deviation is dampened.) That's easy: take those vectors' projections onto each dimension, and normalize them. Combine these normalizing vectors, and multiply all of them by whatever factor gets you the original measures of distance. (Each dimension's normalizing vector will shorten the original vectors, so combining them without a multiplier will lead to a 'shrinking scale' of normal vectors... they'll get smaller and smaller.) After testing a new center, use the old normal vector as the start of the projection, and adjust it according to the new vectors from the newly formed 'hydra' of polygons.

Next, I should address that naive beginning: which points should you test at the very start, before you've accumulated statistics of variation and a normalizing vector? This is just Binary Search - test the very center! For a space in n dimensions, there are 2^n corners, so we don't really want to test all those. In parallel to the Binary Search, testing corners is like guessing '0' or '100'; you don't gain much information, or eliminate much of the space from consideration, when I say that '0 is too low' or '100 is too high'. (Corners don't 'trim the search space') So, for all future test, we let the corners have an implied value equal to the proximity-weighted average of their neighbors, acting as polygon-mesh corners. We avoid testing them, and the natural result is that highest variation is expected at the center of each face of the space. ("Huh?" - on a chess board, each flat edge is a 'face', and it's center is the middle of that edge of the board. On cubes, the face centers are in the middle of each face of the dice. Same idea, in higher dimensions.) Further tests hop to the centers of the faces of each lower dimension, (the center of the cube is followed by the centers of each face, then the midpoints of each edge) as well as into the interiors of the polygons they produce. You'll notice that, as these polygons get smaller, their nested centers will spiral toward the peaks. Check out the diagram, forthcoming. This produces an underlying pattern of search, and gives us a tool for estimating how quickly you'll spiral in on a peak, how quickly you can refine that search, and how quickly your search time becomes divided between different 'hydras' on the search space. Powerful theory follows from this. (Specifics in a separate section on Deep Theory.) For now, I'll mention speed: computing the normalizing vector takes linear time, and so do variation ogive calculations. There are n+1 new polygons created when you test a polygon center, and their yield calculations are linear, too. The whole procedure takes n^2 time, where n is the DIMENSION of the space. That's insanely good news. Double the number of dimensions you're working with, and the work only gets 4 times harder. Moving from 20-, to 40-, to +80-dimensional spaces is well within reach of current processors. Also, while other methods happily test around all 2^n corners, this method starts with the 2n face centers, and moves outward to the face edges, etc, only adding a polynomial number of branches at each layer of resolution. On top of that, each polygon test cuts half of the 'uncertainty' out of its polygon. (The Binary Search, generalized to a measure of constraint of values in the space.) More on uncertainty, and constraint upon values of the space, in Deep Theory. The Deep Theory section will examine the 'search tree', and how 'bushy' it is - how many different hydra-spirals you're following at any one time. (Spoiler: it's very trim, and MAY only increase, on average, as a polynomial of the resolution of the space. My guess is, this will show that 'P=NP on average, but special cases of exponential-time will always exist.' Hmm.)

Notice that, as you build the normalizing vector, your space will stretch and squeeze. This is vital for properly calculating distance-weight of variation, as well as computing accurate centers. If one dimension sees much steeper slopes, on average, distances along that direction are weighted as 'more important' by the normalizing vector, while smooth dimensions are effectively ignored for calculating variation and center. An important addition becomes necessary: whenever a new center has been selected as 'highest potential yield', we need to check if its polygon is kosher. Use the most up-to-date variance ogive and normalizing vector, to check if its yield is still the best, and see if the polygon can be 'swapped' for another, more compact one. (Doing this involves finding the most distant corner of the polygon, looking at the face of the polygon opposite it, and seeing if there are any other tested points closer than the opposing corner to that face . If so, flip the polygon into that space. It's easy math. Diagrams make it easy to see. I wish I could type pictures... Side note: you could also just track the 'non-polygon neighbor vectors' as well - any time two points are closer to each other than they are to the furthest point in their respective polygons, they are a potential source of re-alignment.)

The Software

We'll be keeping track of all the points we've tested for fitness, so far, as well as the centers of polygons that are up for possible testing. Create a list of those points, each point being a set of coordinates and values: the feature coordinates (sugar and cocoa powder mass), fitness coordinates (tastiness response, gathered outside the algorithm from survey, experiments, or models - only tested points have a known fitness, centers are unknown and left blank), an ID number, and the ID numbers of the polygons it forms with neighbors (you numerate these as they appear, '1', '2', '3', etc. These are used to hop between calculations), the ID of the polygon that it was centering, and the expected yield it had, based on that center's variation ogive, distance to polygon corners, and normalizing vector. Every time a new point is added to this list, keep the list sorted by highest expected yield. The first point on the list without a known fitness is the one you test, in each new round of testing. (If you'd like, you could break these into two lists, 'Tested Points' and 'Untested Centers' - it depends on how you set up the array.)

A list of polygons is necessary, as well: their ID number, the ID numbers of the tested points that form its corners, and the ID number of its center are all included. There's also the list of variances, which is just the vectors of deviation from the polygon planes, divided by the distances to their nearest polygon corners. And, as each new polygon 'hydra' expands, the new edges formed are added to the list of edge vectors, for approximating the normalizing vector. So far, that's just 5 lists of vectors. We'll be tossing algebra between them, and going through a single 'for each' loop, and that's it!

Running It

(diagram soon!) With these in hand, we begin the naive testing. Assuming we have a 2-dimensional search space, bounded by the corners (0,0), (1,0), (0,1), (1,1), then the center is our first pick: (0.5,0.5). Once reality-checking returns the fitness of that point, we can move to testing the face centers: (0.5,0), (0,0.5), (0.5,1), (1,0.5). Now, with the fitness of these points, we can average them according to their distance to the corners, and use that as our initial estimate of the corners' 'implied fitness'. (Remember, we aren't going to test those guys!) There are nine points on the space, 5 of known fitness, 4 with implied fitness calculated. Join them all to the points nearest to them, until the space is covered in a polygon mesh. Take the vectors used to join them, as your normalizing vector inputs. Project all of them together onto each dimension, and normalize that 'shadow' of the edges, then combine the projection normals, and solve for the average-distance renormalizing factor. This is your starting estimate of the 'smoothness' or 'ruggedness' of each dimension, and will improve with every new edge created. Meanwhile, those polygons were all added to their list, and you use the normalizing vector to calculate their centers. Add these points to your 'Untested Centers' list, and give them all a dummy 'variance ogive' for now. (Yeah, I guess you could use a normal curve...) Calculate their expected yields, and sort by highest. Whichever one is on top, test.

Once that tested point's actual fitness is returned, here's the order of operations: compare the actual fitness to the polygon plane's estimate, and add that vector to your variance ogive. (The ogive begins to look less and less 'normal'.) Next, construct the edge vectors that join the newly tested point to its surrounding polygon, forming that 'hydra' of n+1 new polygons inside it. Each of those n+1 edges is added to the list of edges, to improve the normalizing vector. Construct each of the new polygons formed this way, add them to the 'Polygon List'. (The group of hydras' computations are the "for each" loop; you find each ones' center & yield, update the lists, and move to the next.) Use the normalizing vector and variance ogive to calculate the center coordinates, and expected yield at those centers. Plop the centers onto the 'Untested Centers' list, keeping the list sorted by highest yield. Pick the highest yield on that list as your next test point. Rinse, repeat.

The theory gets kinda wild, from here, so I'll expand it into a separate page, later. :) Have fun!

Useful Entropy

I should put some information here, before folks get suspicious. Thermodynamics talks about Work - the movement of energy needed to change something. Work isn't energy. It's the movement of hot to cold, the release of tension or pressure, positioned in such a way that it separates hot and cold, or applies tension or pressure, somewhere else. Work takes the gradient between one pair of objects, (hot/cold, in a steam engine) and moves that gradient to another pair (relative motion, for the same case). When we do this 'irreversibly', that means we lost a bit of the gradient. The difference in temperature or pressure you start with is greater than the difference you can create (in a steam engine - to - refrigeration set-up, for example). That's entropy. Stuff leaked, got hot, and wore down - and we can't use it any more, unless we exert more energy. So, we call the part of the gradient that we preserve, 'useful work'. But, is that the only thing in this we can find useful? Now, maybe you're curious. ;)

Entropy has a bad reputation. In common usage, it implies loss, breakage, rust, and the cold, lonely black of a worthless, dead universe. "We started out with a lot of energy for useful work. Now, it's all entropy - useless!" That's not how it is, though. When you're looking at a system, (a bowl of marbles, for example) its 'entropic' state is Whatever State It Tends to Approach. If my marbles are all quiet at the bowl's bottom, time's passage doesn't change them. Because their current state is the same as their future state, we say they're in 'equilibrium'... which is a synonym for 'entropic state'. If I shake the bowl, I'm adding energy (a transfer of gradients, from the chemical tension of my muscles, to the relative motion of the marbles). If I keep shaking the bowl over time, the marbles will KEEP jostling. They are at 'equilibrium' - their present and future are the same. No change in over-all behavior. If I stop shaking, then, as time passes, the marbles will settle to the bottom again. This is 'an increase of entropy'; as the gradient of marble motion transfers to air pressure gradients (sound & wind resistance), the marble behavior changes. Present and future are not alike. The system is 'in flux', and entropy increases until the marbles stop, and present & future are again the same.

More in a bit...

... Sneak Peak at My Outline! ...

Flow of system states sometimes has tendency. Entropic state is patterned. ('Attractors')

Boundary formation is natural across scales. Forces of boundary formation... link to Emergence page.

Linear/Non-linear paths; knowledge of past & future, leverage for change in present (Power of Choice).

Alternate definition of complexity: how quickly does a change in the system cascade through it? how well-specified is each cascade? (specificity -> diagnostic) With this view, brains are complex, static noise isn't.

Intelligence is the ability to detect and respond to changes in your surroundings, in such a way that you continue to exist. ('Fidelity' is continuance of being. Heuristics can have fidelity by chance, intelligence has fidelity by learning to predict its surroundings.) tangent - the existence of psychological triggers for human 'apoptosis' (ahem.) is evidence that we ARE a higher organism than the individuals experiencing it.

Entropic states remain the same unless triggered from outside; they are detectors and transmitters of signal! Use work to create an intelligent equilibrium around you, and the entropic state will keep you posted. That's useful. (Install door bell. Wait for guests. Install tea-pot whistle. Wait for hot water...)

Useful entropy - quickly transmit change of system, along diagnostic paths; amplify these signals as leverage, for your use, and also to preserve system fidelity - higher intelligence! When not in use, it returns to the entropic state. Many systems are at equilibrium; but we can choose the intelligent entropic states, and work to create those. What do you think the biosphere is?

A Wise Shepherd

Ramsey Numbers

No Big Bang

We are already at the universal entropic minimum. Lets make it useful.

Meandering State-Converters

The Black Swan

Tangents & Miscellany

Boeyens & Panspermia

This guy rocks. He doesn't talk about panspermia, but I will. And alchemy, eventually. The footnote on p.180 of Jan Boeyens' "Chemistry from First Principles": "The formulation of spatially separated sigma- and pi-bond interactions between a pair of atoms is grossly misleading. Critical point compressibility studies show [71] that N2 has essentially the same spherical shape as Xe. A total wave-mechanical model of a diatomic molecule, in which both nuclei and electrons are treated non-classically, is thought to be consistent with this observation. Clamped-nucleus calculations, to derive interatomic distance, should therefore be interpreted as a one-dimensional section through a spherical whole. Like electrons, wave-mechanical nuclei are not point particles. A wave equation defines a diatomic molecule as a spherical distribution of nuclear and electronic density, with a common quantum potential, and pivoted on a central hub, which contains a pith of valence electrons. This valence density is limited simultaneously by the exclusion principle and the golden ratio."

More as I meander... and I should get to those diagrams!