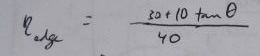Solar Collector Calculations

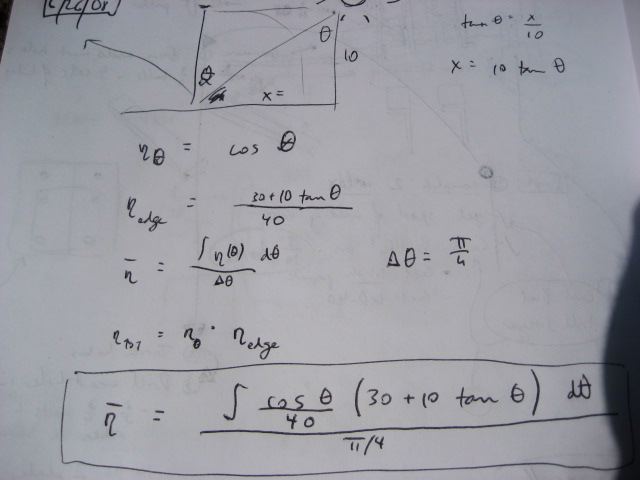
Losses due to edge effects and lack of daily tracking

If we use a passive tracking arrangement for the collector, with only seasonal adjustment, then we have two losses:

1. Loss due to the sun not being perpendicular to the array - if theta is the angle measured from the position of the sun at high noon - then the efficiency stemming from this varies as cosine(theta)
2. Loss due to edge effects - when the sun is not directly overhead, part of the collector tube is not illuminated (assuming length of collector tube is the same as the length of the reflectors)

The overall average efficiency (eta bar) considering these two losses - for the 6 hours of the day around high noon - is:

This value - I estimate to be around 75% - for the average efficiency of the collector without daily tracking.

Someone please run this on the computer or analytically and fill in the exact value.

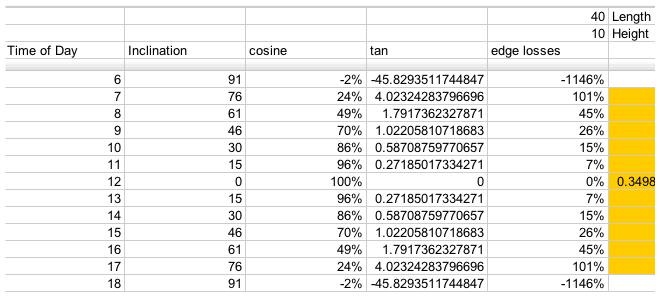
Losses due to edge effects only

For a 40x10 foot solar collector array, with length running East to West, this is a table of losses corresponding to the edge efficiencies (Greek eta_edge) represented by the

term in the above equations:

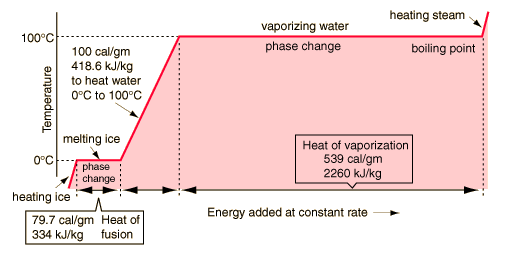
Vapor Generation Rate

Based on water, we have:

heat of vap for water is 40.7 KJ/Mol (i assume room temp numbers are good enough here)

1 Kw = 3600 KJ / Hr

1 mol of water is 18 g

20Kw = 72000 KJ/hr * 1/40.7 Mol/KJ * 18 g/mol

gives 31,842 grams of steam produced per hour, or 70 lb per hour

or thats 1.16 pounds per minute.