Motor selection

The selection of motor includes the following steps (which are described in further detail on this page):

• Step 1) Prerequisite: select Drive Mechanism (Selection guide for this is found in here : Drive mechanism selection.
• Step 2) Select motor type
• Step 3) Define Load requirement
  • Step 3.1) Load calculation
  • Step 3.2) Mechanism calculation (skip to the sub-section that corresponds to the Drive mechanism that was selected as a prerequisite.)
  • Step 3.3) Transmission calculation
• Step 4) Define Motion requirements
• Step 5) Select qualifying motor from product catalog

Step 1) Prerequisites

The prerequisites that shall be met prior to motor selection are listed below:

Prerequisite 1) Select Driven Mechanism

Before selecting a motor, select the Driven Mechanism which can perform the intended output motion when connected to and driven by the motor.

Application factors	Belt drives	Chain drives	Rack/Gear and pinion	Roller Pinon/rack	Leadscrews	Ballscrews	Linear Motors
Accuracy	Low	Low	Low-High	High	Low	Low-High	High
Backlash/Vibration	A consideration	A consideration	A consideration	Near Zero	A consideration	A consideration	Near Zero
Acceleration	Medium	Low	High	High	Low	Medium	High
Speed	Medium	Low	Medium	High	Low	Medium	High
Load capacity	Low	Medium	High	High	Low	High	Low
Length	Shorter	Shorter	Long	Long	Shorter	Shorter	Moderate
High wear and short life	A consideration	A consideration	A consideration	Long life	A consideration	A consideration	Long life
Maintenance	A consideration	A consideration	A consideration	Low to none	A consideration	A consideration	Low to none
Noise level	Medium	High	Medium	Low	High	Medium	Low
Dust and dirt emissions	High	High	Moderate	Low to none	Moderate	Moderate	Low to none

Prerequisite 2) Identify the available power supply

Identify the available Mains Electricity (also called Utility Power or Wall Power) for the intended location of the machine. Lists of Mains Electricity standards by country is readily available on the internet.

Most countries is typically around 100 or 200 Volts for residential voltage and around 400 for three-phase voltage.

Servo motors are available for these voltages: 100, 200 and 400 Volts.

Step 2) Select the motor type

Step 2.1) Identify application and desired motor attributes

Use the table below to select one of four motor types that correspond to your application and the desired motor attributes.

Attribute	Stepper motors	Servo motors	Brushed DC motors	Brushless DC motors
Area of use	Positioning by incremental steps. Low speed and low acceleration.	High speed and high acceleration.	Continuous rotation at high RPMs and constant torque across the motor’s speed range.	Continuous rotation at high RPMs and constant torque across the motor’s speed range.
Suitable applications	• floppy disk drives • flatbed scanners • computer printers • plotters • slot machines • image scanners • compact disc drives • intelligent lighting • camera lenses • CNC machines and 3D printers • Textile machines • Printing presses • Medical imaging machinery • Small robotics • Welding equipment	• Automated manufacturing • Robotics • CNC machinery • Telescopes • Elevators • Conveyor Belts • Camera Auto Focus • Solar Tracking System • Metal Cutting & Metal Forming Machines • Antenna Positioning • Printing Presses/Printers • Automatic Door Openers	• Home appliances • toys • electrical propulsion • cranes • paper machines • steel rolling mills	• Drones • Electric cars • Washing machines • Air Conditioners • Cordless tools • Computer • Fans • Disk drives
Accuracy	High	High (achieved by adding encoder to the system.)	None	Varies
Torque at low speeds	High	High	-	-
Torque at high speeds	Low (can lose up to 80% torque at high speeds)	High	-	-
Cost efficiency	High	Lower (uses rare-earth magnets, may need encoder or gearbox.)	High	Lower
Lifespan	Long life	Shorter	Shorter	-
Size	Compact	High output power relative to size and weight.	Compact	-
Load capacity	Low (might skip steps at high loads.)	High	-	-
Efficiency	Low (constantly draw maximum current independent of load.)	High (80–90% efficiency.)	High	-
Ease of use	• Easily controlled (can be controlled with micro controllers such as the ATmega chips that are readily available on Arduino development boards.) Can stall or lose position without a control loop.	• Higher maintenance if gearbox and encoder is included. • Limited range of motion; positional rotation servos are limited to 180 degrees of motion. • Works in AC or DC drive.	• Torque to Speed Ratio can be altered (exclusive to brushed motors.) • High maintenance requirements due to easily worn out as a result of continuous moving contact.	• Some brushless motors are difficult to control and require a specialized regulator. • Low maintenance.

Step 2.2) Confirm Load characteristic

Look at the Load characteristics type in the table below and identify which Load characteristic corresponds to your application. Then confirm that the motor type you selected from the table above corresponds to the identified Duty cycle.

Load characteristic	Application examples
Torque that is constant	conveyors, extruders, bulk material conveyors, extruders, positive displacement pumps
Torque that changes abruptly	elevators, compactors, punch presses, saws, and batch conveyors
Torque that change gradually over time	centrifugal pumps, fans, blowers, compressors with unloaders

Step 2.3) Confirm Duty cycle type

Look at the Duty cycle types in the table below and identify which Duty cycle corresponds to your application. Then confirm that the motor type you selected from the table above corresponds to the identified Duty cycle.

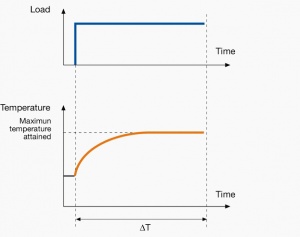
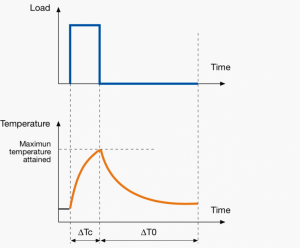
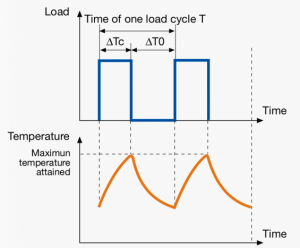
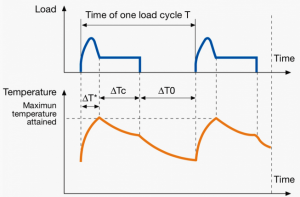
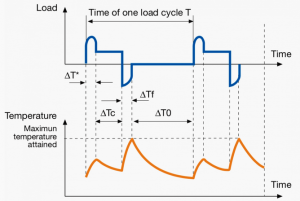
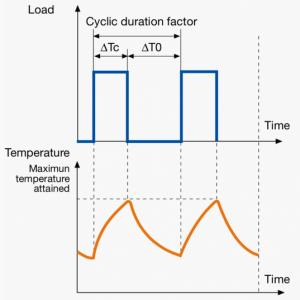
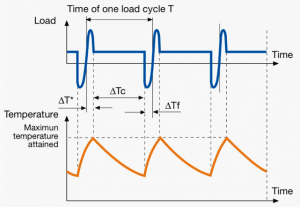
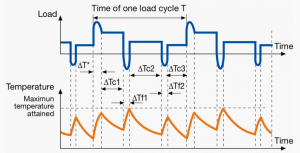
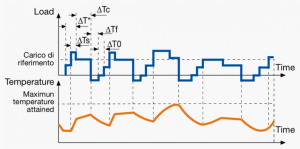
A duty cycle type specifies the sequence and time duration the motor operation including Starting, Running with no load, Running with a full load, Electric braking, and Rest. How the operations affect motor temperature determines whether increased cooling is needed or whether another motor is suitable.

In the table below, the term "Load" refers to the electrical current (measured in Ampere) that is supplied. This electrical load, or current, corresponds to the mechanical load, or torque, measured in Newton meter. More torque requires more current. The terms "Temperature equilibrium" or "Steady state temperature" simply mean temperature that remains constant.

Type	Full designation	Cycle name	Description	Load and temperature curve	Applications
S1	S1	Continuous duty	The motor is turned on and works at a constant Load for enough time to reach Temperature equilibrium. It then keeps going. An example could be a fan that is turned on and kept on.		Fans, escalators, eMobility solutions, packaging machinery, paper mill drives compressors, conveyers, centrifugal pumps.
S2	Duty type followed by duration of the duty, e.g. S2 40 minutes.	Short-time duty	Constant load but not long enough to reach Temperature equilibrium (unlike S1) and instead enters a rest period long enough for the motor to cool down to ambient temperature.		Crane drivers, drives for household appliances, sluice gate drives, valve drives and machine tool drives.
S3	Duty type followed by cyclic duration factor, e.g. S3 30%.	Intermittent periodic duty	Sequential, identical Run and Rest cycles. The load is constant. Temperature equilibrium is not reached. Unlike S2, the rest periods are not long enough for the motor to cool down to ambient temperature.		Plastics machinery, food and beverage processing.
S4	Duty type followed by cyclic duration factor, moment of inertia of the motor JM, and by the moment of inertia of the load JL (both refer to the motor shaft) e.g. S4 20% JM = 0.15 kg m2 JL = 0.7 kg m2.	Intermittent periodic duty with starting	Sequential, identical Run and Rest cycles. The load is constant but starting uses more current which leads to a rise in temperature. Neither Run and Rest periods are long enough to attain Temperature equilibrium.		Metal cutting, drilling tool drives, mine hoist drives for lift trucks.
S5	Duty type followed by cyclic duration factor, moment of inertia of the motor JM, and by the moment of inertia of the load JL (both refer to the motor shaft) e.g. S5 20% JM = 0.15 kg m2 JL = 0.7 kg m2.	Intermittent periodic duty with electric braking	Sequential, identical cycles of Starting, running at constant load, a quick electric braking period, and a period de-energized and at rest. Thermal equilibrium is not reached in one duty cycle. Braking is done electrically and is quick.. No rest periods.		Several machine tool drives, drives for electric suburban trains and mine hoist.
S6	Duty type followed by cyclic duration factor e.g. S6 30%.	Continuous operation with intermittent load	Sequential, identical cycles of running with constant load and running with no load. No rest periods (unlike S3). Thermal equilibrium is not rached in one duty cycle.		Pressing, cutting, shearing and drilling machine drives.
S7	Duty type followed by moment of inertia of the motor JM and the moment of inertia of the load JL (S7 JM = 0.4 kg m2 JL = 7.5 kg m2).	Continuous operation with electric braking	Sequential identical cycles of starting, running at constant load and electric braking. No rest periods.		Blooming mills for steel manufacturing, supply chain machinery across material handling, some medical technologies, including precision applications.
S8	Duty type followed by moment of inertia of the motor JM, moment of inertia of the load JL, load, speed and cyclic duration factor, for each speed condition (S8 JM = 0.7 kg m2JL = 8kgm2 25kW 800rpm 25% 40kW 1250rpm 20% 25 kW 1000 rpm 55%).	Continuous operation with periodic changes in load and speed	Identical duty cycles, each consisting of a time of operation at constant load corresponding to a predetermined speed of rotation, followed by one or more times of operation at other constant loads corresponding to different speeds of rotation. No rest periods.
S9	S9	Duty with non-periodic load and speed variations	Motor is run non-periodically with varying load and speed within the permissible operating range. This duty includes frequently appplied overloads which may greatly exceed the reference load.
S10	Duty type followed by per unit quantities p/Δt for the partial load and its duration, per unit quantity TL which represents the thermal life expectancy of the insulation system related to thermal life expectancy in case of duty type S1 with rated output, and by quantity r which indicates load for a time de-energized and at rest, e.g. S10 p/Δt = 1.1/0.4; 1/0.3; 0.9/0.2; r/0.1 TL = 0.6.	Duty with discrete constant loads and speeds	A specific number of discrete values of load maintained for a sufficient time to allow the machine to reach thermal equilibrium. The minimum load during a duty cycle may have value zero and be relevant to a no- load or rest condition.

Step 3) Define Load requirement

Now that we have selected the motor type, the motor has to be dimensioned. That means we need to conclude how powerful the motor must be in order to perform the intended task. If the motor is under-dimensioned, it won't be powerful enough to perform the intended task. If the motor is over-dimensioned, it's price and operation cost will be too high.

These are the sub-steps for dimensioning the motor:

• Step 3.1) Load calculation
• Step 3.2) Mechanism calculation
• Step 3.3) Transmission calculation

Dimensioning the motor can either be done manually or by using a Motor Dimensioning Software (also referred to as motor selection software.)

Step 3.1) Load calculation

The Load is constituted by

• The Mass of the object that the motor is intended to move (this does not include the mechanism which is covered in the next step.)
• External Forces that will require more work to be performed by the motor.

Note the Mass of the object that motor is intended to move.

Note any External Forces that will require more work to be performed by the motor.

Step 3.2) Drive mechanism calculation

The motor must not only be strong enough to move the Load - it must be strong enough to move the Mechanism the the Load is applied to. For example, if the application is a belt conveyor intended to move boxes from one end to another, the motor will have to be strong enough to move the boxes that together make up the Load (covered in the step above), plus the Mechanism which includes the belt as well as the wheel that drives the belt.

Depending on the type of Drive mechanism, there are usually two parameters of interest:

• the Mass of the mechanism and
• the Moment of Intertia of the mechanism

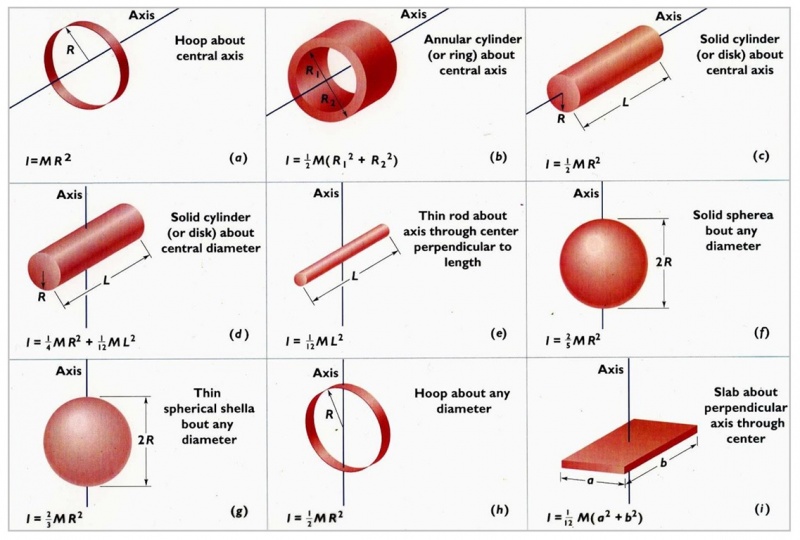
Moment of Inertia is a measurement of how much effort is required to rotate an object. The Moment of Inertia for an object is determined by:

• The rotational axis relative to the object
• The shape and size of the object
• The mass of the object

Jump to the sub-chapter corresponding to the selected drive according to the list below:

Mechanism	Jump to step
Belt Drive	Step) 3.2.1
Ball Screw	Step) 3.2.2
Chain and Sprocket	Step) 3.2.3
Rack and Pinion	Step) 3.2.4
Linear Motor	Step) 3.2.5
Roll Feeder	Step) 3.2.6
Rotational Table	Step) 3.2.7
Crank	Step) 3.2.8

Step) 3.2.1 Belt Drive

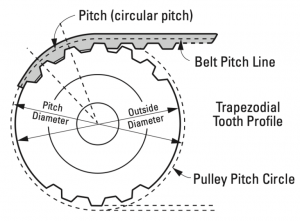
In a Belt Drive the motor is coupled to a timing pulley that drives a flexible toothed belt, with its coupled load, back and forth between two idler pulley guides.

Step) 3.2.1.1 Note pitch diameter

The Driver Pitch Diameter is slightly larger than the outer diameter of the pulley and corresponds to the pitch line of the belt which is the line formed by the belt’s tensile cord.

The Pitch Diameter value can be used to calculate a rotational to linear ratio as given by:

V = ω * (D / 2)

where

V = rotational to linear ratio

D = Pitch Diameter

ω = the angular speed measured in radians per second

Step) 3.2.1.2 Note Belt Mass

Belt Mass is the mass of the belt including any objects that are moving the load linearly. The Load (calculated in Step 4.1) is excluded from belt mass.

Step) 3.2.1.3 Note Driver/Idler Inertia

Driver/Idler Inertia is the inertia of the mechanism that moves the load. This includes any rotationally moving parts that are not a part of the motor or transmission.

Step) 3.2.1.4 Note Efficiency

Mechanical efficiency is measured as the ratio of the measured performance to the performance of an ideal machine. It is entered as a value between 0 and 1. See chapter "List of typical mechanical efficiencies" in this article.

Step) 3.2.2 Ball Screw

A ball screw is coupled to a rotary motor and causes linear motion between a rotating screw and its non-rotating nut.

Step) 3.2.2.1 Note Lead

The Lead is a measurement of the distance that the Load will move linearly with a single full revolution of the screw. The Lead for different ball screws can be found in product catalogs and are normally specified in millimeters.

Step) 3.2.2.2 Note Slide Mass

Slide Mass is the mass of the slide including any objects that are moving the load linearly. The Load (calculated in previous steps) is excluded from this mass.

Step) 3.2.2.3 Note Ball Screw Inertia

A Ball Screw has a cylindrical shape and will rotate around its central axis and can therefore be calculated like this:

I = 1/2 * m * r^2

where

I = Moment of Inertia

m = Mass

r = Radius

For a graphical explanation, see figure C in the chapter "Table of equations for Moment of Inertia for different shapes" in this article.

If the mass is not known, the following formula can be used:

I = (π/32) * D^4*ρ*L

where

I = Moment of Inertia

ρ = Density for the material that the Ball Screw is made from

L = Length

Step) 3.2.2.4 Note Coupling Inertia

If Couplings are attached to the Ball Screw, their Moment of Inertia must be factored in the same way as for the Ball Screw covered in the step above.

Step) 3.2.2.5 Note Efficiency

Mechanical efficiency is measured as the ratio of the measured performance to the performance of an ideal machine. It is entered as a value between 0 and 1. See chapter "List of typical mechanical efficiencies" in this article.

Step) 3.2.3 Chain and Sprocket

A chain and sprocket is a rotary motor coupled to a sprocket wheel that drives a linked chain, with its coupled load, back and forth between idler sprocket guides.

Step) 3.2.3.1 Note Sprocket Pitch Circle Diameter

Sprocket Pitch Circle Diameter is a measure of the diameter that the chain moves about. This value is used to calculate a rotational to linear ratio as given by:

V = ω * (D / 2)

where

V = rotational to linear ratio

D = Pitch Diameter

ω = the angular speed measured in radians per second

Step) 3.2.3.2 Note Chain Mass

Chain Mass is the mass of the chain including any objects that are moving the load linearly. The Load (calculated in previous steps) is excluded from this mass.

Step) 3.2.3.3 Note Sprocket/Idler Inertia

Sprocket/Idler Inertia is the inertia of the mechanism that moves the load. This includes any rotationally moving parts that are not a part of the motor or transmission.

Step) 3.2.3.4 Note Efficiency

Mechanical efficiency is measured as the ratio of the measured performance to the performance of an ideal machine. It is entered as a value between 0 and 1. See chapter "List of typical mechanical efficiencies" in this article.

Step) 3.2.4 Rack and Pinion

A rack and pinion is a rotary motor coupled to a toothed pinion wheel that engages a toothed rack to create relative motion between the two elements.

Step) 3.2.4.1 Note Pinion Pitch Circle Diameter

Pinion Pitch Circle Diameter is a measure of the diameter that the rack moves about. This value is used to calculate a rotational to linear ratio as given by:

V = ω * (D / 2)

where

V = rotational to linear ratio

D = Pitch Diameter

ω = the angular speed measured in radians per second

Step) 3.2.4.2 Note Rack Mass

Rack Mass is the mass of the Rack including any objects that are moving the load linearly. The Load (calculated in previous steps) is excluded from this mass.

Step) 3.2.4.3 Note Pinion Inertia

Pinion Inertia is the inertia of the mechanism that moves the load. This includes any rotationally moving parts that are not a part of the motor or transmission.

Step) 3.2.4.4 Note Efficiency

Mechanical efficiency is measured as the ratio of the measured performance to the performance of an ideal machine. It is entered as a value between 0 and 1. See chapter "List of typical mechanical efficiencies" in this article.

Step) 3.2.5 Linear Motor

Linear motors are either iron-core and ironless motors that directly create linear thrust. Their separate sections (coil and magnet channel) produce relative motion between a carriage and its base along linear bearing guides.

Step) 3.2.5.1 Note Force margin

Force margin (Km) – This is a coefficient for cases that have increased required force to accelerate or decelerate. This is based on the structure of a machine. Input a value of 1 or more based on the inertia of the moving coil and the center of gravity of load. Force to accelerate or decelerate is calculated as F = Km·m·a.

Step) 3.2.5.2 Note Slide Mass

Slide Mass is the mass of the slide including any objects that are moving the load linearly. The Load (calculated in previous steps) is excluded from this mass.

Step) 3.2.6 Roll Feeder

A Roll Feeder is a mechanism that continuously feeds material through rollers.

Step) 3.2.6.1 Note Driver Pitch Diameter

Driver Pitch Diameter is a measure of the diameter that the material moves about. This value is used to calculate a rotational to linear ratio as given by:

V = ω * (D / 2)

where

V = rotational to linear ratio

D = Pitch Diameter

ω = the angular speed measured in radians per second

Step) 3.2.6.2 Note Driving Roller Inertia

Driving Roller Inertia is the inertia of the roller that moves the material.

Step) 3.2.6.3 Note Driven Roller Inertia

Driven Roller Inertia is the inertia of the roller(s) that freely spin with the material. This includes any rotationally moving parts that are not being driven by the motor. If the pitch diameters of the rollers differ from that of the driving roller the ratio between the two must be factored in.

Step) 3.2.6.4 Note Efficiency

Mechanical efficiency is measured as the ratio of the measured performance to the performance of an ideal machine. It is entered as a value between 0 and 1. See chapter "List of typical mechanical efficiencies" in this article.

Step) 3.2.7 Rotational Table

A rotational table is a mechanism where the primary load is moving rotationally. There is no mechanism coupling the load to the motor/transmission.

Step) 3.2.8 Crank

The crank mechanism translates rotational motion of the crank arm into reciprocating linear motion via a connecting rod.

Step) 3.2.8.1 Note Crank Radius

Crank Radius is the radius from the center of rotation to the pin that connects to the connecting rod.

Step) 3.2.8.2 Note Connecting Rod Length

Connecting Rod Length is the distance from the pin that connects to the crank to the pin that connects to the load.

Step) 3.2.8.3 Note Crank Inertia

Crank Inertia is the inertia of the mechanism that moves the load. This includes any rotationally moving parts that are not a part of the motor or transmission.

Step) 3.2.8.4 Note Efficiency

Mechanical efficiency is measured as the ratio of the measured performance to the performance of an ideal machine. It is entered as a value between 0 and 1. See chapter "List of typical mechanical efficiencies" in this article.

Step 3.3) Select gearing

In a lot of machines, the motor is capable of much higher speeds than required. At the same time, a motor may not be able to provide the required torque. Therefore, gearing is applied to the motor.

When selecting gearing for a motor, the gearing is commonly refereed to as a Reducer, which can also be referred to as a Gear Reducer, Speed Reducer, or Gearbox. It consists of a number of mated gears. A Reducer is connected to a motor and uses the mechanical advantage of gears to enable the following functions:

• Reduce speed
• Increase torque

A reducer's rated output torque, that is the torque that the reducer is capable of delivering, shall exceed the required torque of the intended application. Otherwise, the reducer can break or performance can decline rapidly.

The Gear ratio can be calculated like this:

Gear ratio = motor speed / required speed

For example, a motor with a speed of 500 rpm and a gearbox with a 10:1 gear ratio would result in and output speed of 50 rpm.

Then the new required torque must be calculated like this:

New required torque = initial required torque / gear ratio

Gearbox Output Torque can be calculated with the following equation:

Output Torque = Motor Output Torque * Gearbox Ratio * Gearbox efficiency

See Gear for additional info and gear calculation.

Step 4) Define Motion requirements by defining Motion profile

Besides defining the Load requirement (in earlier steps), we must also define the requirement for the Motion of the drive-mechanism carrying that Load. Just because a motor can provide enough torque for a mechanism to move an object that weighs 20 kilos doesn’t necessarily mean it is able to do so in a restricted time frame of 3 seconds over a distance of 400 mm. Therefore we must define such motion requirements via something called a Motion profile.

A Motion profile is a representation of a Drive-mechanism’s movement, or motion requirements, over time in the form of graphs for any of the following variables:

• Position
• Velocity (measured in m/s or mm/s, etc.)
• Acceleration
• Jerk

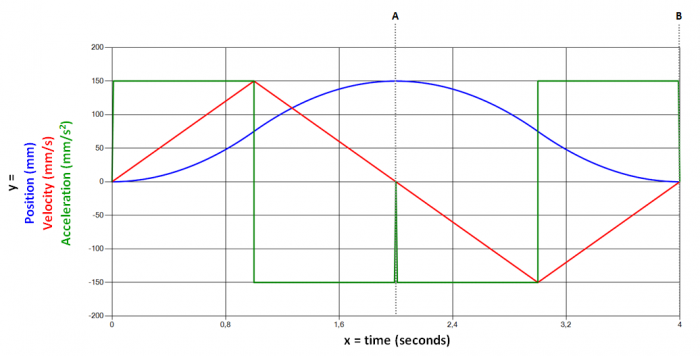
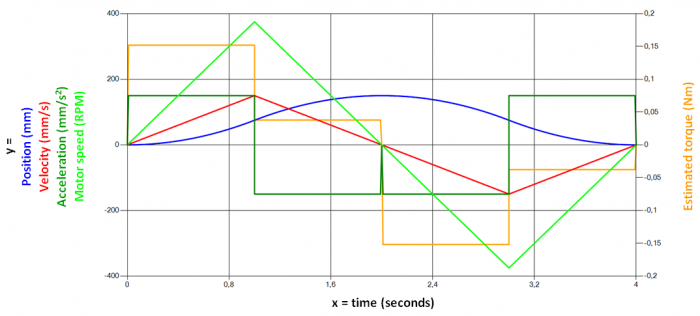
In the example below we see a motion profile for a Slide in a ball screw mechanism. To generate the graphs in the picture, the following requirements were specified:

A) First, from a stand-still, we want the Slide to carry the Load 150 mm in no more than 2 seconds. This position is reached middle of the profile, where it can be read from the blue graph that the Slide has reached it’s max position of 150 mm in 2 seconds. From the red graph, it can be read that the velocity is back at a stand-still; 0 mm/s.

B) After that, we want that motion reversed in the same amount of time; -150 mm in 2 seconds. Just after the dotted line A, we can read from the red graph that the Slide is now speeding up in the reverse direction, represented by negative values in mm/s. At the end of the profile, when another 2 seconds has passed, we can read from the blue graph that the Slide has returned to it’s orginal position of 0 mm. The table below shows the input for the Motion profile graphs. (The ”Type” indicated as ”Triangle” is explained below the graphs.)

Type	Time (s)	Position (mm)	External force
N/A; starting position	0	0	0
Triangle	2	150	0
Triangle	4	0	0

It is common among motor selection softwares to include the functionality of displaying graphs for

• Motor speed
• Estimated torque

superimposed over other motion profile graphs. Below is a motion profile identical to the one above but with Motor speed (measured in revolutions per minute) and Estimated torque (measured in Newton meter)

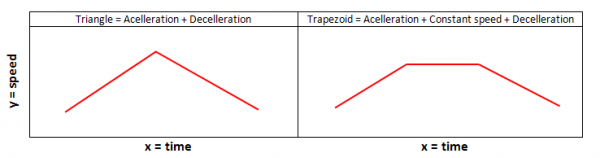
In the context of a Motion profile, motion can take the following three forms:

In practice, these forms of motion are commonly combined into two main profiles:

The Triangle profile represents acceleration from a stand-still to max speed, followed by deceleration back to a stand-still.

The Trapezoid profile represents acceleration from a stand-still to a max speed that remains constant for some time, followed by deceleration back to a stand-still.

The example profile above is a combination of two triangles, where the second triangle is ”upside down” as the slide is moving in the opposite direction, back to it’s original position.

A motion profile can be any combination of accelerations, constant speeds, and deceleration.

Step 5) Select qualifying motor from product catalog

The final step is to access a motor product catalog and select a motor that fulfills the requirements that were defined in the previous steps. Most motor selection software have such a product catalog embedded in the software where you can filter motors that are with or without a brake, or have an appropriate voltage for your geographical location, etc.

List of typical mechanical efficiencies

· Acme-screw w/brass nut ~ 0.35 - 0.65

· Acme-screw w/plastic nut ~ 0.50 - 0.85

· Ball-screw ~ 0.85 - 0.95

· Preloaded Ball-Screw ~ 0.75 - 0.85

· Spur or Bevel Gears ~ 0.90

· Timing Belts ~ 0.96 - 0.98

· Chain & Sprocket ~ 0.95 - 0.98

· Worm Gears ~ 0.45 - 0.85

Table of equations for Moment of Inertia for different shapes

Moment of Inertia is a measurement of how much torque is required to rotate an object. The Moment of Inertia for an object is determined by:

• The rotational axis relative to the object
• The shape and size of the object
• The mass of the object