Gear

Introduction

Gears, just like spurs and sprockets, are mechanisms used to transfer energy by rotary motion.

They can all be used to change the following:

• Direction of rotation
• Speed
• Torque

Gears are used to trade rotational speed for torque or vice versa. In other words, in gearing there is an inverse relationship between rotational speed and torque.

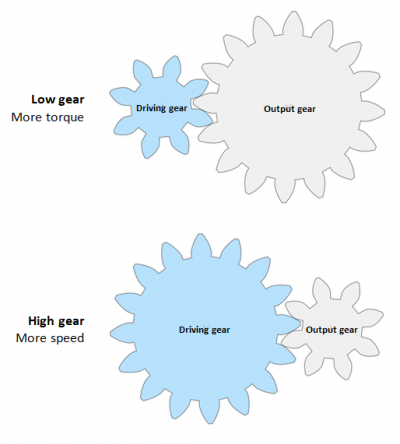
The Input gear, also known as the Drive gear, is connected directly to a motor (or the pedals on a bike) and drives the Output gear.

In lower gear, the Drive gear is smaller than the Output gear and for example rotates a bike wheel slower but with more torque to get you up a hill.

In higher gear, the Drive gear is bigger than the Output wheel and rotates the wheel with lower torque but faster rotational speed.

	Drive Gear	Output Gear	Torque	Speed
Lower gear:	Smaller	Bigger	Stronger	Slower
Higher gear:	Bigger	Smaller	Weaker	Faster

Types of Gears

The table below provides a comparison of a number of gear types. The parameters used are described below the table unless self-explanatory.

Gear type	Image	Applications	Axes condition	Efficiency Range	Ratio range	Max Speed	Max Load	Smooth, quiet operation	Prevents Thrust Force	Cost efficiency	Comments
Spur		Small conveyors Farm machinery Automotive, aircraft and trains Pumps Household appliances Washers and dryers	Parallell	94-99.5%	1:1 to 6:1	Mid	Mid	No. Less at high speeds.	Yes	High	High precision. The most common type of gear.
Helical		Medium to large conveyors Mixers Large pumps Water treatment Crushers	Parallell	94-99%	3:2 to 10:1	High	High	Considerably	No	Mid	If gears have a Double helical design, thrust force is prevented. If they have Single helical design, it is not. Thrust force must be accommodated by thrust bearings. Teeth are twisted either clockwise or counter-clockwise.
Straight bevel		Medium to large conveyors Mixers Crushers Water treatment Machine tool equipment Printing machines Differentials	Intersecting	93-97%	3:2 to 5:1	Low	Mid	No	Partly	Mid	Out of the bevel gears, it has the simplest design and highest manufacturability. Generally used in relatively slow speed applications (less than 2m/s circumferential speed). They are often not used when it is necessary to transmit large forces. Cone-shaped gear body.
Spiral bevel		Medium to large conveyors Mixers Crushers Water treatment Automotive, aircraft and trains Pumps Washers and dryers	Intersecting	95-99%	3:2 to 4:1	High	High	Very	No	Low	Excellent accuracy, strength and abrasion resistance. Due to greater tooth area, they can deliver more torque than other gears of the same size and move faster than other gears, producing greater output in less time. Cone-shaped gear body, spiral teeth.
Zerol		Medium to large conveyors Mixers Crushers Water treatment	Intersecting	95-99%	3:2 to 4:1	High	Very high	Very	Partly	Low	Can rotate in both directions unlike Spiral bevel gears. High precision. A special type of spiral bevel gears where the spiral angle is zero at the middle of the face width. Combined of advantages of straight and spiral bevel gears. Teeth are curved but lie in the same direction as straight bevel gear teeth.
Miter		Automobiles Printing presses Power plants Cooling towers Marine applications Steel plants	Intersecting	98-99%	1:1	Mid - High	High	Very	No	Mid - Low	A special type of bevel pair of where the gears have an equal number of teeth and hence a gear ratio of 1:1. Therefore they cannot be used to change speed or torque - they are only used to change direction. They are mated at a pitch cone angle of 45°. Manufacturability is High for straight teeth and Low for spiral teeth.
Hypoid		Truck rear axle gearbox Small to medium conveyors Small mixers Crushers Water treatment	Non-parallel, non-intersecting	80-95%	10:1 to 200:1	Very high	Very high	Extremely	No	Low	Generally used where speeds exceed 1000 rpm (although above 8000 rpm, ground gears are recommended). Also useful for lower speed applications requirng extreme smoothness or quiet operation. Hypoid gears differ from spiral bevel gears in that the gear axes does not intersect; the picture shows how the axle of the gear is not pointed towards the center of the mated gear. The curved teeth are shaped along a hyperbola - hence the name hypoid gear.
Rack and pinion		Automobiles (steering systems) Stairlifts Actuators Trains Large gantry robots Lifting mechanisms Positioning mechanisms Material handling	Parallell	94-99.5%	-	Mid	High	No	Yes	High	Can have either straight or spiralled teeth. The DFM (Design for Manufacturing) is Low if the teeth are helical. Converts rotational motion to linear motion or vice versa.
Screw		Machine tools Water pumps Mixers Automobiles	Non-parallel, non-intersecting	70-95%	1:1 to 6:1	Mid	Low	Very	No	Mid	A type of Helical gear. A pair of Screw gears usually mated at 90° to each other but other angles are possible.
Worm		Small conveyors Package handling equipment Farm machinery Lifts and elevators Material handling systems Automobiles (steering systems)	Non-parallel, non-intersecting	30-90%	5:1 to 100:1	Mid	Very high	Extremely	No	Mid	A special type of screw gear. The most the smooth, quiet and compact gear system. Good for high shock load applications but offer low efficiency. Can have a self-locking ability where the screw can turn the gear but the gear is prevented from turning the screw. Used to greatly increase torque or greatly reduce speed in low to medium speed application.

Gear parameter explanations

Axes condition

An axis is the cylinder which a gear is applied to. The axis condition describes how two axes for a mated gear pair are oriented relative to each other. There are three types of Axes conditions:

• Parallel: both axes which the two gears are attached to run parallel to each other.
• Intersecting: the theoretical center-lines going through the center of the two center holes of the gears intersect.
• Non-parallel and non-intersecting: the theoretical center lines of the axis are not parallel and do not intersect.

The possible axes condition for the gear types in the table above can be identified by picturing axes running through the center holes of the gears in the images.

Efficiency Range

No system is 100% efficient but losses in efficiency will require more input power for the motor driving the gears and possibly a more powerful and expensive motor to achieve the required torque. Efficiency range refers to the span between the typical minimum and maximum efficiencies for the respective gear types.

Ratio range

Gear ratio (GR) is the ratio between the rotational speeds of two mating gears. The Ratio range spans from the minimum appropriate gear ratio to the maximum.

Max Speed

Speed can either be measured in RPM (Revolutions per Minute) or in meters per second. There are low, mid, and high velocity gears:

• Low: <3 m/s
• Mid: 3 - 15 m/s
• High: >15 m/s

Max Load

Max load refers to the amount of torque that the respective gear types can deliver without breaking or wearing out quickly. Besides gear type, the max load will depend on the material and the size along with the Gear Module (explained further down in this article.) In the table above, gears of the same material, size and module is assumed.

Thrust Force prevention

Thrust force is unintentional force along the axis to which a gear is applied. Thrust forces can be mitigated by applying thrust bearings to axes.

Cost efficiency

Cost efficiency is tied to the simplicity of the design of a gear and in turn its manufacturability. Gears with more advanced design that are harder to fabricate will cost more.

Gear materials

Mated gears should be made from different materials to avoid abrasion and scoring.

Below are some common gear materials and their properties:

• Cast iron: low cost, low precision.
• Steel: high cost, high hardness and tensile strength
• Nylon: low cost, non-corrosive properties, not suitable for high load applications.
• Brass: low cost, high precision, not suitable for high load applications.
• Aluminum: low cost, not suitable for high load applications.

Contact Ratio

The contact ratio (ε) measures the average number of teeth in contact at all times. Mating gears should always have the same size teeth (the same parametric pitch.) The best contact ratio must be larger than 1.2 to ensure the ability to transmit high loads, offer rigidity to the transmission and allow for a silent and uniform operation.

Gear ratio calculation

The latest stable version of the Open Source Ecology Gear calculator is found here:

OSE Gear calculator

Gear ratio (GR) is the ratio between the rotational speeds of two mating gears. It can be be calculated with the following formulas:

GR = n1/n2 = d1/d2 = τ1/τ2 = ω2/ω1

where

n = number of teeth

d = diameter

τ = torque

ω = velocity

The number 1 following the symbol indicates that we are referring to the driven gear (or output gear). The number 2 following the symbol indicates that we are referring to the driving gear (or input gear). For example: n1 = number of teeth of the output gear. τ2 = the torque of the input gear.

Note that for the fraction containing velocity ω, the input is divided by the input, whereas this is reversed for the other fractions.

When selecting a Gearbox (also known as Gear Reducer, Speed Reducer or simply Reducer) for a motor, the Gear Ratio can be calculated like this:

Gear Ratio = Motor Speed/Required Speed

Then the New required torque must be calculated like this:

New Required Torque = Initial Required Torque/Gear Ratio

Gear ratio calculation examples

Two mating gears

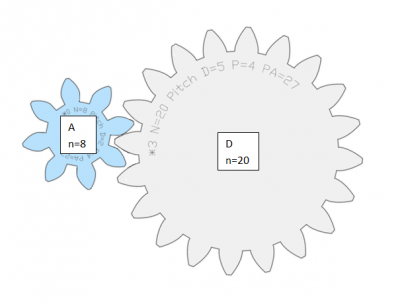
The gear ratio (GR) between the driving gear A and the driven gear D shown in the picture below is calculated as follows:

Gear ratio between gears A and D = number of teeth of D / number of teeth of A;

GR,AD = nD/nA = 20/8 = 2.5

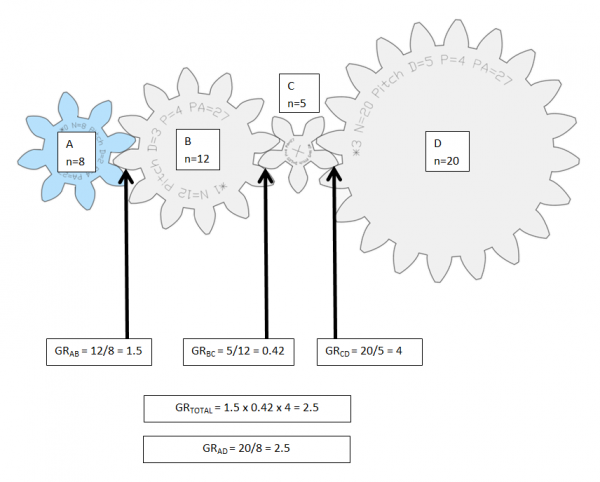
Gear train with Idler gears

To calculate the total gear ratio of a gear train (a set of two or more connected gears), the gear ratios of each pair is multiplied.

In other words, if we have a train of four gears, A, B, C, and D, (as in the image below) the total ratio is calculated by multiplying the gear ratio between

• A & B,
• B & C, and
• C & D, so that

GR,total = GR,AB x GR,BC x GR,CD = nB/nA x nC/nB x nC/nD = 12/8 x 5/12 x 20/5 = 2.5

However, all gears except the first gear (Driver) and the last gear (Output) can be disregarded and the results will still be the same; GR,AD = 2.5 (just like the example above with only two gears.) That is because all gears are connected to their own individual axis. The fact that none of the gears share an axis makes the gears in between the first and the last gear so called Idler gears. No matter the size or the number of Idler gears put in between the Input and Output gear, it will not affect the total gear ratio of the gear train. That is because each idler gear will be used as Input in one fraction followed by a fraction where the same gear is instead used as an Output so that it cancels itself out.

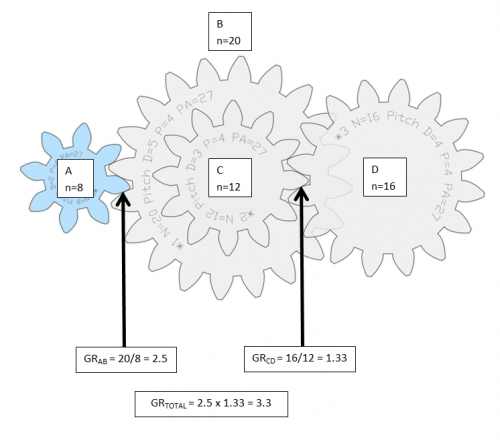
Compound gear train

In this example, gear B and C share axis. Therefore the gears in between the Input gear and the last gear cannot be ignored as in the example above. Instead the gear ratio of each gear pair must be multiplied to calculate the total gear ratio: GR,total = GR,AB x GR,CD = nB/nA x nC/nD = 20/8 x 16/12 = 2.5 x 1.33 = 3.3

See also

OSE Gear calculator

[List of Machine element calculators]

External links

https://geargenerator.com (the gear illustrations in this article were created using website.)