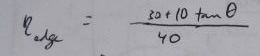Solar Collector Calculations: Difference between revisions

From Open Source Ecology
Jump to navigation Jump to search
No edit summary
Line 62: Line 62:
'''Mass Flow'''= 5.64 g/s or 44 lb/Hour
'''Mass Flow'''= 5.64 g/s or 44 lb/Hour


==Generating Steam at 180C/350F==
if change in temp is 150C, corresponding to producing steam at 180C and roughly 10 atm (140 psi) then the mass flow is 7.07 g/s or 56 lb/Hour


'''Specific heat of water''': 1 Cal/g/C = 1 kCal/kg/C = 4 kJ/kg/C
== Superheating Steam ==
 
'''Heat of Vaporization''': 2270 kJ/kg


Superheating the steam requires an additional input of energy
'''Specific heat of steam''': 1/2 Cal/g/C = 2 kJ/kg/C
'''Specific heat of steam''': 1/2 Cal/g/C = 2 kJ/kg/C
To raise water from 20C to 180C, which would be a good working pressure of 10 atmospheres or 140 psi [http://www.engineeringtoolbox.com/saturated-steam-properties-d_457.html]
'''Heating of water from 20 to 100C''' - 320 kJ/kg
'''Vaporization''' - 2270 kJ/kg
'''Raising steam temperature from 100 to 180C''' - 160 kJ/kg
'''Total''' - 2750 kJ/kg
We have 20 kW available, or 72,000 kJ/hr -
(72,000 kJ/hr)/(2750 kJ/kg) = 26 kg/hour
'''Steam generation rate is 26 kg/hour, or 58 lb/hr'''

Revision as of 21:57, 28 June 2008

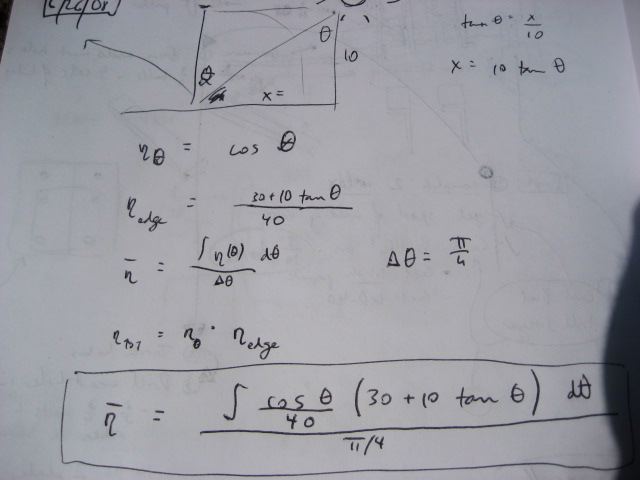
Losses due to edge effects and lack of daily tracking

If we use a passive tracking arrangement for the collector, with only seasonal adjustment, then we have two losses:

  1. Loss due to the sun not being perpendicular to the array - if theta is the angle measured from the position of the sun at high noon - then the efficiency stemming from this varies as cosine(theta)
  2. Loss due to edge effects - when the sun is not directly overhead, part of the collector tube is not illuminated (assuming length of collector tube is the same as the length of the reflectors)

The overall average efficiency (eta bar) considering these two losses - for the 6 hours of the day around high noon - is:

Collector efficiency.jpg

This value - I estimate to be around 75% - for the average efficiency of the collector without daily tracking.

Someone please run this on the computer or analytically and fill in the exact value.

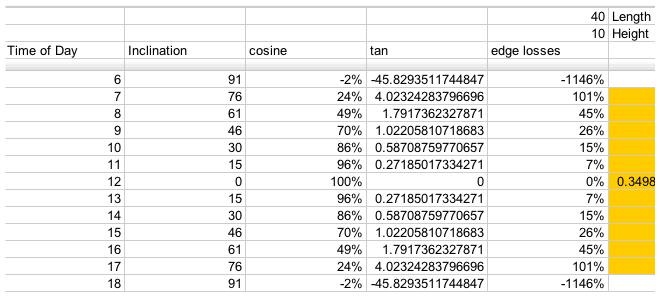
Losses due to edge effects only

For a 40x10 foot solar collector array, with length running East to West, this is a table of losses corresponding to the edge efficiencies (Greek eta_edge) represented by the

Edge losses equation.jpg

term in the above equations:

Edge losses.jpg

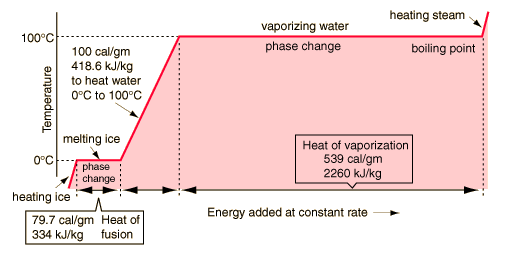
Vapor Generation Rate

Based on water, we have:

Phases of water.gif


generating steam

the energy needed to heat a mass of water is given by:

E = M * Specific heat * change in temp

The Energy needed to vaporize a mass of water is given by:

E = M * heat of vaporization

The energy needed to raise the temperature of the water and then vaporize it is the sum of the two. Because we are dealing with power instead of energy, we can replace mass by the mass flow (g/S).

Power = Massflow * (Specific heat * change in temp + Heat of vap)

or

Massflow = P / (Specific heat * change in temp + Heat of vap)


for our specific case:

Power = 20,000 J/s (20 Kw)

Change in temp = 300 C (from room temperature to 330 C)

specific heat= 4J/g

heat of vaporization=2,226 J/g


Mass Flow= 5.64 g/s or 44 lb/Hour

if change in temp is 150C, corresponding to producing steam at 180C and roughly 10 atm (140 psi) then the mass flow is 7.07 g/s or 56 lb/Hour

Superheating Steam

Superheating the steam requires an additional input of energy

Specific heat of steam: 1/2 Cal/g/C = 2 kJ/kg/C

Retrieved from "https://wiki.opensourceecology.org/index.php?title=Solar_Collector_Calculations&oldid=2333"