Gear
Introduction
Gears, just like spurs and sprockets, are mechanisms used to transfer energy by rotary motion.
They can all be used to change the following:
- Speed of rotation
- Direction of rotation
- Amount of torque available to do work
Gears can be used to trade rotational speed for torque or vice versa. In other words, in gearing there is an inverse relationship between rotational speed and torque.
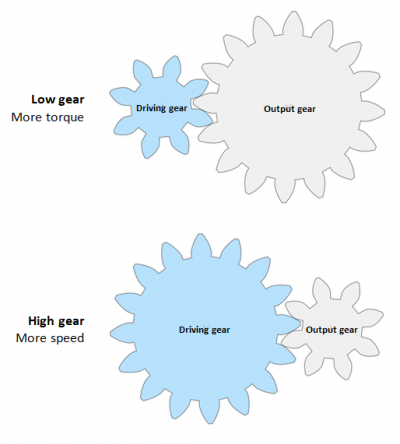
The Input gear, also known as the Drive gear, is connected directly to a motor (or the pedals on a bike) and drives the Output gear.
In lower gear, the Drive gear is smaller than the Output gear and for example rotates a bike wheel slower but with more torque to get you up a hill.
In higher gear, the Drive gear is bigger than the Output wheel and rotates the wheel with lower torque but faster rotational speed.
| Drive Gear | Output Gear | Torque | Speed | |
|---|---|---|---|---|
| Lower gear: | Smaller | Bigger | Stronger | Slower |
| Higher gear: | Bigger | Smaller | Weaker | Faster |
Types of Gears
aaa
| Gear type |
Applications | Axes condition | Efficiency Range |
Ratio range |
Max Speed |
Max Load |
Smooth, quiet operation |
Prevents Thrust Force |
DFM | Cost efficiency |
Comments |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Spur | Small conveyors Package handling equipment Farm machinery Planetary gear sets Automotive, aircraft and trains Pumps Watering systems Household appliances Washing and drying machines Material handling systems |
Parallell | 94-99.5% | 1:1 to 6:1 |
Mid | Mid | No. Less at high speeds. |
Yes | High | High | High precision. The most common type of gear. |
| Helical | Medium to large conveyors Mixers Large pumps Water treatment Crushers |
Parallell | 94-99% | 3:2 to 10:1 |
High | High | Considerably | Single helical design: No Double helical design: Yes |
Mid | Mid | The thrust force along the axis of the gear must be accommodated by appropriate thrust bearings. Teeth are twisted at an angle, either clockwise or counter-clockwise, around the circular gear body. |
| Straight bevel | Medium to large conveyors Mixers Crushers Water treatment Machine tool equipment Printing machines Differentials |
Intersecting | 93-97% | 3:2 to 5:1 |
Low | Mid | No | Somewhat | Mid | Mid | Out of the bevel gears, it has the simplest design and highest manufacturability. Generally used in relatively slow speed applications (less than 2m/s circumferential speed). They are often not used when it is necessary to transmit large forces. Cone-shaped gear body. |
| Spiral bevel |
Medium to large conveyors Mixers Crushers Water treatment Automotive, aircraft and trains Pumps Watering systems Household appliances Washing and drying machines Material handling systems |
Intersecting | 95-99% | 3:2 to 4:1 |
High | High | Very | No | Low | Low | Excellent accuracy, strength and abrasion resistance. Due to greater tooth area, they can deliver more torque than other gears of the same size and move faster than other gears, producing greater output in less time. Cone-shaped gear body, spiral teeth. |
| Zerol | Medium to large conveyors Mixers Crushers Water treatment |
Intersecting | 95-99% | 3:2 to 4:1 |
High | Very high |
Very | Somewhat | Low | Low | Can rotate in both directions unlike Spiral bevel gears. High precision. A special type of spiral bevel gears where the spiral angle is zero at the middle of the face width. They have the combined of advantages of straight and spiral bevel gears. The teeth of zero bevel gears are curved but lie in the same direction as the teeth of straight bevel gears. They can rotate in both directions unlike Spiral bevel gears. |
| Miter | Automobiles Printing presses Power plants Cooling towers Marine applications Steel plants |
Intersecting | 98-99% | 1:1 | Mid - High |
High | Very | No | Low to Mid |
Mid - Low |
A special type of bevel pair of where the gears have an equal number of teeth and hence a gear ratio of 1:1. Therefore they cannot be used to change speed or torque - they are only used to change direction. They are mated at a pitch cone angle of 45°. DFM (Design for Manufacturing) is High for straight teeth and Low for spiral teeth. |
| Hypoid | Rear axles gearboxes for large trucks Small to medium conveyors Small mixers Crushers Water treatment |
Non-parallel, non-intersecting | 80-95% | 10:1 to 200:1 |
Very high |
Very high |
Extremely | No | Low | Low | Generally used where speeds exceed 1000 rpm (although above 8000 rpm, ground gears are recommended). They are also useful, however, for lower speed applications that require extreme smoothness of motion or quiet operation. Hypoid gears differ from spiral bevel gears in that the gear axes does not intersect; the picture shows how the axle of the gear is not pointed towards the center of the mated gear. The curved teeth are shaped along a hyperbola - hence the name hypoid gear. |
| Rack and pinion | Automobiles (steering systems) Stairlifts Actuators Trains Large gantry robots Lifting mechanisms Positioning mechanisms Material handling |
Parallell | 94-99.5% | - | Mid | High | No | Yes | High | High | Can have either straight or spiralled teeth. The DFM (Design for Manufacturing) is Low if the teeth are helical. Converts rotational motion to linear motion or vice versa. |
| Screw | Machine tools | Non-parallel, non-intersecting | 70-95% | 1:1 to 6:1 |
Mid | Low | Very | No | Mid | Mid | A type of Helical gear. A pair of Screw gears usually mated at 90° to each other but other angles are possible. |
| Worm | Small conveyors Package handling equipment Farm machinery Lifts and elevators Material handling systems Automobiles (steering systems) |
Non-parallel, non-intersecting | 30-90% | 5:1 to 100:1 |
Mid | Very high |
Extremely | No | Mid | Mid | The most the smooth, quiet and compact gear system. Good for high shock load applications but offer low efficiency. Can have a self-locking ability where the screw can turn the gear but the gear is prevented from turning the screw. Used to greatly increase torque or greatly reduce speed in low to medium speed application. A special type of screw gear. The pair consists of a circular gear (worm wheel) and a screw-shaped gear (worm.) |
Contact Ratio
The contact ratio (ε) measures the average number of teeth in contact at all times. Mating gears should always have the same size teeth (the same parametric pitch.) The best contact ratio must be larger than 1.2 to ensure the ability to transmit high loads, offer rigidity to the transmission and allow for a silent and uniform operation.
Gear ratio calculation
The latest stable version of the Open Source Ecology Gear calculator is found here:
Gear ratio (GR) is the ratio between the rotational speeds of two mating gears. It can be be calculated with the following formulas:
GR = n1/n2 = d1/d2 = τ1/τ2 = ω2/ω1
where
n = number of teeth
d = diameter
τ = torque
ω = velocity
The number 1 following the symbol indicates that we are referring to the driven gear (or output gear). The number 2 following the symbol indicates that we are referring to the driving gear (or input gear). For example: n1 = number of teeth of the output gear. τ2 = the torque of the input gear.
Note that for the fraction containing velocity ω, the input is divided by the input, whereas this is reversed for the other fractions.
When selecting a Gearbox (also known as Gear Reducer, Speed Reducer or simply Reducer) for a motor, the Gear Ratio can be calculated like this:
Gear Ratio = Motor Speed/Required Speed
Then the New required torque must be calculated like this:
New Required Torque = Initial Required Torque/Gear Ratio
Gear ratio calculation examples
The images for the calculation examples below were generated by using this website: https://geargenerator.com
Two mating gears
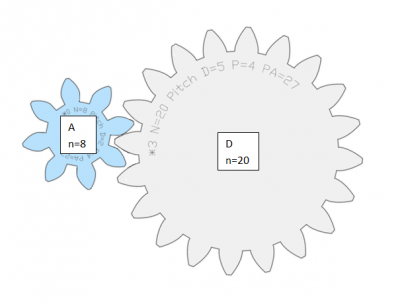
The gear ratio (GR) between the driving gear A and the driven gear D shown in the picture below is calculated as follows:
Gear ratio for gear A and D = number of teeth of D / number of teeth of A;
GR,AD = nD/nA = 20/8 = 2.5
Gear train with Idler gears
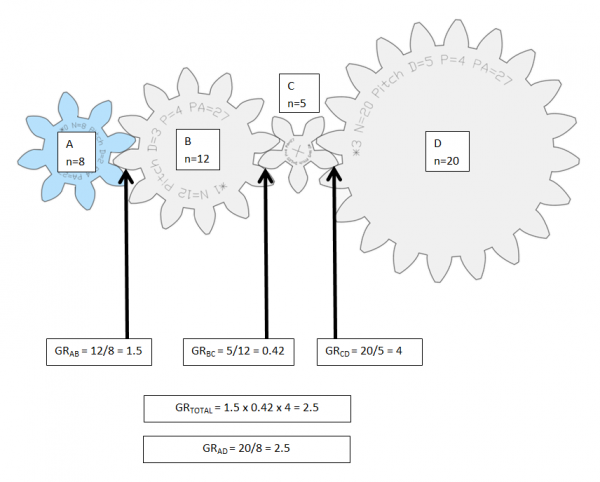
To calculate the total gear ratio of a gear train (a set of two or more connected gears), the gear ratios of each pair is multiplied.
In other words, if we have a train of four gears, A, B, C, and D, (as in the image below) the total ratio is calculated by multiplying the gear ratio between
- A & B,
- B & C, and
- C & D, so that
GR,total = GR,AB x GR,BC x GR,CD = nB/nA x nC/nB x nC/nD = 12/8 x 5/12 x 20/5 = 2.5
However, this example can be calculated exactly as the one above it and the results are identical; GR,AD = 2.5. That is because all gears are connected to their own individual axis and because the Input gear A and the Output gear D have the same number of teeth as in the example above. The fact that none of the gears share an axis makes the gears in between the first and the last gear so called Idler gears. No matter the size or the number of Idler gears put in between the Input and Output gear, it will not affect the total gear ratio of the gear train. That is because each idler gear will be used as Input in one fraction followed by a fraction where the same gear is instead used as an Output so that it cancels itself out.
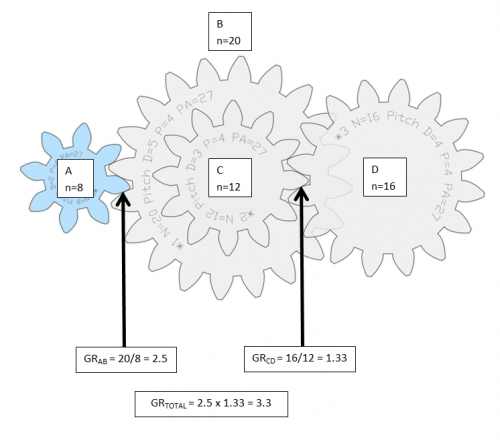
Compound gear train
In this example, gear B and C share axis. Therefore the gears in between the Input gear and the last gear cannot be ignored as in the example above. Instead the gear ratio of each gear pair must be multiplied to calculate the total gear ratio: GR,total = GR,AB x GR,CD = nB/nA x nC/nD = 20/8 x 16/12 = 2.5 x 1.33 = 3.3
See also
External links
https://geargenerator.com (the gear images in this article were created using website.)