Hole Puncher Calculations
Overview
 Ironworker Hole puncher calculations.
Ironworker Hole puncher calculations.
Calculations
Force Required to Shear the metal
According to an Ironworker Blade manufacturer (he prefers not to be mentioned by name) with a 6 degree rake in the blade, you can shear 1"x10" steel with 100 tons of force.
No data has been found regarding how much force to shear 1"x12" as is the desired spec for the machine, so we will assume that there is a direct relaitonship between length of cut and force to shear it. Following this logic, 100T/10"=xT/12" Solving for x, we get Force to shear 1"x12"=120T.
We will include a safety factor to account for any errors we have made. A force of 130T or more should suffice.
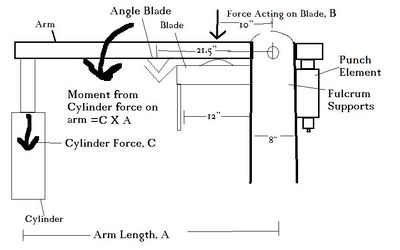
The required moment to act on blade
To find this, we must make a few basic assumptions:
- The fulcrum supports are 8" wide
- The blade is 12" wide and placed as close as possible to the fulcrum supports.
- The force will be applied at the center of the blade and distributed evenly.
- The angle blade, and the flat blade are mounted on the same mount.
Blade moment
Since the force on the blade(B) is known, as is its distance from the fulcrum, we can calculate the necessary moment, M. M=Force(B) x Distance from the pivot(d) (10")
For the capability of cutting 1"x12", B=130 tons.
- M=130 tons x 10" = 1300 inch tons
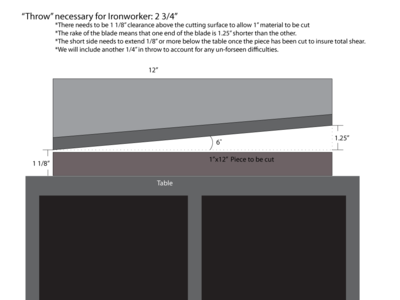
Throw Requirements
Throw is the vertical movement required for the blade. In this case, It's 2.75".
Calculating the arm length and cylinder size
The arm length will control how many times magnification we get from the cylinder force.
- If building an ironworker whose max cutting ability is under 1" x 12", you could scale the cylinder size down according to your desires.
Since the such high force is required to shear the desired metal, we will use the 6" bore cylinder with a 12" stroke available at surplus center.
Arm length must satisfy throw and force requirements. Force generates a minimum arm length requirement, whereas throw generates a maximum arm length.
- Throw requires that the cylinder rod is long enough, or spaced properly, so that the blade has enough vertical movement. This is effected adversely by arm length. IE, the longer the arm is, the longer rod you will need.
- Force requires that the lever arm is long enough to magnify the force from the cylinder to enough to shear the metal. The longer the arm is, the less force you will need.
Minimum Arm Length
To calculate the arm length using this cylinder, we must set the cylinder force (C) multiplied by the lever arm length (A) equal to the required moment (M), so A X C = M. Solving for A, we get A=M/C
In this particular design, the cylinder will be contracting while shearing, which means the cylinder tonnage we are using must be on the contracting side. See Cylinder Tonnage Calculations for how to find the contracting strength. The calculated contracting tonnage (C) for this specific cylinder is 31.8 tons.
So, A= 1300inT/31.8T =
A =40.86" Minimum.
Maximum Arm Length
This is calculated by the ratios of throw to rod length and arm length. The distance (D) any point on the arm travels is inversley related to its distance (L) from the fulcrum. Or: D1/L1=D2/L2. 1 corresponds to the cylinder, and 2 corresponds to the blade. L1=12", as it is the rod length on the cylinder. L2=2.75", as it is the required throw for the blade. D2 is 10", the distance from the blade to the fulcrum. D1 is unknown.
Solving for D1, we get D1= D2L1/L2= 10"*12"/2.75"= 43.63"=A max
Design 2
In this design, the cylinder is expanding while shearing the 1"x12", so we use the expanding cylinder tonnage for the 8" bore cylinder, or 75.36 tons.
A=M/C For the capability of cutting 1"x12", M=4800 Inch tons.
- A=4800 inch tons/ 75.36 tons = 63.69 inches
For the capability of cutting 1"x10", M= 4000 inch tons
- A=4000 inch tons / 75.36 tons = 53.08 inches
We should also double check to make sure the punch still has enough power We must find the required punch moment, and insure it is less than the required blade moment.
- M= Punch force (P) x distance (d). P= 150 tons, d=23"
M= 150 tons x 23" = 3450 inch tons. This is less than the blade moment, so we are OK.
Design analysis
As we can see, both designs are going to require really long overall arms. Here are the calculated lengths:
Design 1 will require A+6", including the end amounts (this depends on how close the cylinder attaches to the end, and how far the punch is away from the end).
- 6x6= 91.3"+6" = 97.3 inches
- 4x4, 12"= 84.9"+6" = 90.9" including the end amounts.
- 4x4, 10"= 70.7"+6" = 76.7", including the end amounts.
Design 2 will require A+23", including the end amounts.
- For 12": 63.36+23"= 96.36", including the end amounts.
- For 10": 53.08+23"= 66.08", including the end amounts.
Calculation of the size of the pin
To find the size of the pin, we must first find how much force is acting on it when it is most stressed. In this case, it is when we are cutting thru the 1"x10" metal.
Since the arm is not accelerating upwards, we can do a statics calculation, and assume the sum of all the forces is zero. So: -31.5T+400T+P=0 Solving for P, we get P=368.5T.
Now, we must use this to find the necessary cross sectional area of the pin to prevent it from warping.
- At each side, where the pin goes thru the pin holders, a force of P/2 is applied to it via the fulcrum supports. This means that there is a shear force of P/2, or 184.25T acting on the pin.
- The allowable shear for A36 steel is 7.2TSI.
- To calculate the radius of the pin, we must set the product of the cross sectional area (A) and the allowawble shear (S) equal to the shear force (P/2). or, AxS=P/2
- We can replace A with PixR^2, since the cross sectional area is a circle. So PixR^2xS=P/2. Solving for R, we get R=Root[(P/2)/Pi/S]
- Plugging it all in, we get R=Root[184.25T/3.14/7.2TSI]=2.86"
- To find the diameter of the pin, we simply multiply Rx2. so D=5.71
Now that's a big pin!