Steam Engine Efficiency

Introduction

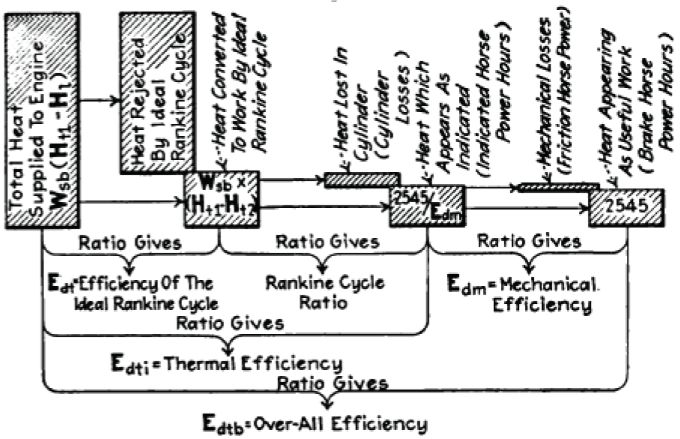
Start with definition of terms. Here is a chart showing relationships of various efficiency standards for a steam engine: (source:[1], Chapter 10. There are some compounds over 26% overall efficiency and some singles running over 14%. Reportedly, 20% efficiency was obtained (another reference), but it had very low cutoff ratio and couldn't tolerate load changes. That is where the electronic steam valve comes in to achieve this.)

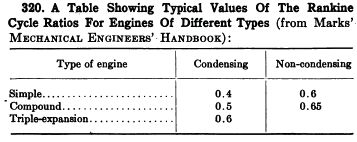
The same reference has these typical Rankine cycle ratios for engines of different types:

Steam Engine Efficiency Predictions for the Factor e Farm Solar Power Generator

Updated 2.1.09

The missing link to date on the Factor e Farm solar power generator is the heat engine. Our goal is to develop a steam engine with Milestone 1 thermal efficiency of 17%, and Milestone 2 efficiency of 26%. The latter involves the use of electronic valving for total control of steam injection. Steam injection timing is called the cutoff ratio. As an analogy, this is comparable to electronic fuel injection in internal combustion engines.

Efficiency Predictions of Steam Engine

The basic efficiency of a heat engine is governed by the Carnot Cycle. For our case, we will operate at 650 K [2] (377C, or 710F), the practical upper bound due to blackbody radiation losses for our case.

This is the practical upper limit:

For our case, we take Carnot efficiency = (650K - 363K)/650K = 44%

for the case of going from 377C to 90C. The Rankine cycle ratio of .4 is proven for simple steam engines - so our worst case efficiency scenario is 17.6%. If we subtract 10% from this for mechanical efficiency losses - then we obtain about 16% efficiency. With steam injection electronic valving, we can approach the triple-expansion engine efficiency - .6 Rankine cycle ratio - or steam engines with 26.4 thermal efficiency. Cylinder insulation should cover cylinder heat loss, and perfect control of steam injection should allow for near-complete extraction of usable energy from steam.

=Examples of Documented Solar Concentrator Power Cycle Efficiencies

Examples of steam cycle efficiencies are shown here for several solar thermal concentrator power plants.

The most relevant for our work is the Shenandoah steam power plant, with cycle efficiency of 17%, or 40% of Carnot efficiency. The high and low temperatures here were 382C and 110C, or a Carnot efficiency of:

(655K - 383K)/655K = 42%