Steam Engine Efficiency
Main > Energy > Steam Engine
Introduction
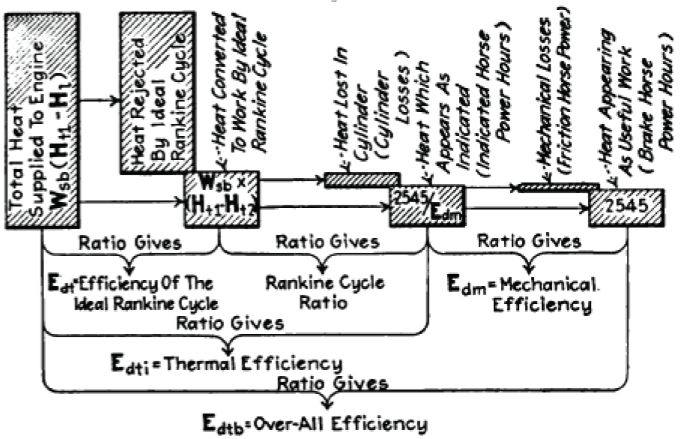
Start with definition of terms. Here is a chart showing relationships of various efficiency standards for a steam engine: (source:[1], Chapter 10. There are some compounds over 26% overall efficiency and some singles running over 14%. Reportedly, 20% efficiency was obtained (another reference), but it had very low cutoff ratio and couldn't tolerate load changes. That is where the electronic steam valve comes in to achieve this.)
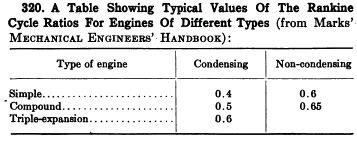
The same reference has these typical Rankine cycle ratios for engines of different types:
Steam Engine Efficiency Predictions for the Factor e Farm Solar Power Generator
Updated 2.1.09
The missing link to date on the Factor e Farm solar power generator is the heat engine. Our goal is to develop a steam engine with Milestone 1 thermal efficiency of 17%, and Milestone 2 efficiency of 26%. The latter involves the use of electronic valving for total control of steam injection. Steam injection timing is called the cutoff ratio. As an analogy, this is comparable to electronic fuel injection in internal combustion engines.
Efficiency Predictions of Steam Engine
The basic efficiency of a heat engine is governed by the Carnot Cycle. For our case, we will operate at 650 K [2] (377C, or 710F), the practical upper bound due to blackbody radiation losses for our case.
This is the practical upper limit:
For our case, we take Carnot efficiency = (650K - 363K)/650K = 44%
for the case of going from 377C to 90C. The Rankine cycle ratio of .4 is proven for simple steam engines - so our worst case efficiency scenario is 17.6%. If we subtract 10% from this for mechanical efficiency losses - then we obtain about 16% efficiency. With steam injection electronic valving, we can approach the triple-expansion engine efficiency - .6 Rankine cycle ratio - or steam engines with 26.4% thermal efficiency. Cylinder insulation should cover cylinder heat loss, and perfect control of steam injection should allow for near-complete extraction of usable energy from steam.
As the last step, we have a 95% efficienct generator, for a total of about 15% efficiency for the steam - electrical cycle.
Overall Efficiency of Solar Generator
We have shown in Solar_Collector_Losses_Summary that the solar collector/boiler efficiency is 47%. We multiply this by 16% efficiency of the steam engine cycle - and obtain an overall system efficiency of 7.5%. This will give us 3.6 kW of power as milestone that reaches the $1/watt materials cost prediction.
Comparison to Others
- The Solar One power tower showed an overall 14% efficiency.
- The Nevada Solar One parabolic trough system showed an overall efficiency of 6.5% and a cost of $3.9 per watt.
- Others - here
- The most relevant for our work is the Shenandoah steam power plant, with cycle efficiency of 17%, or 40% of Carnot efficiency.
- Ausra compact linear Fresnel reflectors showed up to at 69 bar and 285C - peak 39% overall efficiency from sun to electricity. See First Results from Compact Linear Fresnel Reflector Installation, by D.R. Mills et al - downloadable here
- Paper shows over 300 kW obtained from about 1350 kW of solar intercept
- Note: carnot efficiency here = (658K-348K)/658K = 47%. Ausra is operating with near perfect reflection and near zero thermal losses.
- Ausra results are spectacular, and Ausra made a claim that it could power the entire USA
Relevance to Factor e Farm Prototype
By utilizing the same strategy of compact linear fresnel reflectors and similar operating temperatures, we are aiming to achieve an efficiency about 1/5 that of Ausra, while still making the economics work out.
Power towers are likely to be more expensive because each heliostat must be supported and controlled individually. Solar troughs don't produce sufficient concentration to gain the advantages of CLFR arrays.
Main > Energy > Solar Power > Solar Turbine
Main > Energy > Steam Engine