LifeTrac IV/Research Development/Carrying capacity
Overview
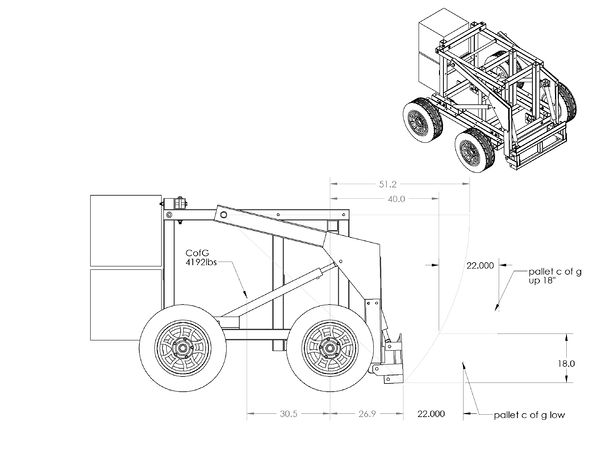
This page provides information for the approximate carrying capacity before vehicle tipping. Additional information is desired to determine structural strength when loaded. Operating load is defined as 50% of the tipping load.
C of G Analysis
- Weight is approximate to +/- 200lbs
- Tipping load is calculated by summing the moments around the front axle
Force Distribution Analysis
Wanted: Formulas for calculating the force distribution as a function of arm angle
- Assume symmetric along center plane
- LifeTrac image in MS Word file
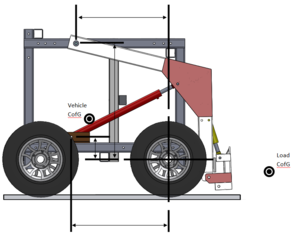
- Basically what we need is an understanding between carried load CofG, vehicle CofG, arm pivot location, hydraulic cylinder mounted location and the front wheel which acts as the point to tip around.
- Keep everything in x-y coordinate system for the initial static analysis and then provide the formula as a function of load location as it arcs around the loader arm pivot point at the top of the frame.
- The end goal is to have a formula that can be applied to any design
- Add whatever additional considerations are required to make the analysis more accurate
- Please provide definitions of variables used, easily understood diagram and formulas
- If uploading to wiki is a problem, please email data to Mike Apostol directly
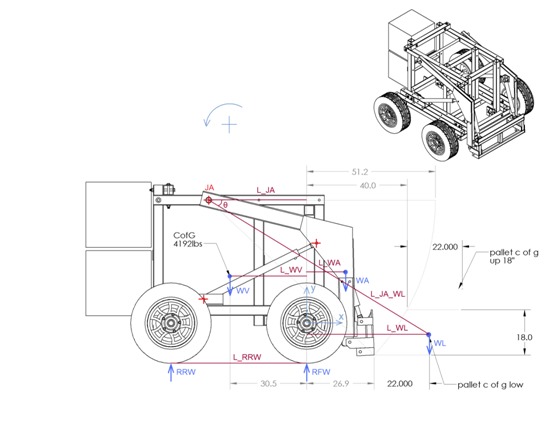
Tipping load calculations
WL: Weight of load (pallet)
WA: Weight of arm
WV: Weight of vehicle (without the weight of arm)
RFW: Reaction force at the front wheels
RRW: Reaction force at the rear wheels
L_WL: The distance between the c of g of the pallet (where WL is applied) and the vector y
y: The vertical vector that passes through the axis of the front wheels
JA: The position of the joints that support the arm on the frame of the vehicle
L_JA_WL: The distance between the joint of the arm and the c of g of the pallet
θ: The angle between the L_JA_WL and the horizontal
RFW is the summation of the reaction forces applied to the two front wheels. I do not include the weight of the arm in the weight of the vehicle, because the position of the center of gravity of the arm changes while the arm rises. The same might be considered for the hydraulic cylinders, in more detailed calculations.
Balance of momentums:
L_WV*WV – L_RRW*RRW – L_WL*WL – L_WA*WA = 0
where,
L_WL = L_JA_WL*cos(θ) – L_JA
Similar equation can be found for L_WA. Negative value of the L_WA implies that the c of g of the arm lies on the left side of the vector y.
The vehicle is tipping when RRW=0. Thus the tipping load is:
WL_tipping = (L_WV*WV – L_WA*WA)/L_WL
For any WL, the reaction force on each wheel of the rear axis is the half of RRW, where:
RRW = (L_WV*WV – L_WL*WL – L_WA*WA)/L_RRW
The balance of forces implies that:
– RRW – RFW + WV + WL + WA = 0
Therefore, the reaction force on each wheel of the front axis is 0.5*RFW, where:
RFW = WV + WL + WA – RRW
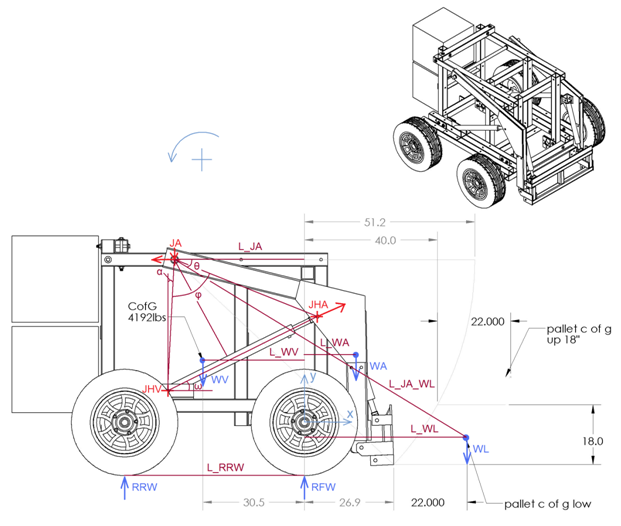
Calculations of the static force on the joint of the arm
JA: The joint between the arm and the frame of the vehicle
JHV: The joint between the hydraulic cylinder and the frame of the vehicle
JHA: The joint between the hydraulic cylinder and the arm
R_JAy: The force applied from the vehicle to the arm, at vertical direction
R_JAx: The force applied from the vehicle to the arm, at horizontal direction
R_JHA: The force applied from the hydraulic cylinders to the arm
R_JHAy: The vertical component of the force applied from the hydraulic cylinders to the arm
R_JHAx: The horizontal component of the force applied from the hydraulic cylinders to the arm
ω: The angle between the direction of the hydraulic cylinder and the horizontal
L_JA_JHV: The distance between the positions of the joint JA and the joint JHV
L_JA_JHA: The distance between the positions of the joint JA and the joint JHA
L_JHV_JHA: The current length of the hydraulic cylinder (from joint JHV to joint JHA)
The force R_JHA is always in the direction of the axis of the hydraulic cylinder. That is because the joints of the cylinder cannot transmit momentums at the direction of z.
(90deg – ω – α) is the angle between the L_JA_JHV and the L_JHV_JHA (i.e. the angle that has as a tip the joint JHV and as ends the joints JHA and JA).
sin(90deg – ω – α)/L_JA_JHA = sin(φ)/L_JHV_JHA =>
cos(ω+α)/L_JA_JHA = sin(φ)/L_JHV_JHA =>
cos(ω+α) = sin(φ)*L_JA_JHA/L_JHV_JHA =>
ω = arccos(sin(φ)*L_JA_JHA/L_JHV_JHA) – α
Balance of the momentums applied at the arm (calculated at the position of JA):
L_JA_JHV* sin(90deg – ω – α)*R_JHA – (L_JA + L_WL)*WL – (L_JA + L_WA)*WA = 0 =>
L_JA_JHV*cos(ω+α)*R_JHA – (L_JA + L_WL)*WL – (L_JA + L_WA)*WA = 0
Thus, the force applied from the hydraulic cylinders to the arm is:
R_JHA = ( (L_JA + L_WL)*WL + (L_JA + L_WA)*WA )/( L_JA_JHV*cos(ω+α))
The vehicle is symmetric, so each of the two cylinders applies a force to the arm that equals to 0.5*R_JHA.
The balance of forces at the vertical direction gives:
R_JAy = R_JHA*sin(ω) – WL – WA
The balance of forces at the horizontal direction gives:
R_JAx = R_JHA*cos(ω)
The total force R_JA is:
R_JA = ( (R_JAx)^2 + (R_JAy)^2 )^0.5
This force is distributed equivalently to the two joints between the arm and the frame of the vehicle. Thus, 0.5*R_JA is applied to each joint. If there is no bending on this cylindrical joint, the maximum shear stress is:
τ_shear = (4/3)*F/A
where F = 0.5*R_JA is the applied force and A = pi*r^2 is the cross-sectional area of the pin (that has radius r) of the joint. pi is 3.14.
The equivalent tensile stress is:
σ_total = 2*τ_shear
This equivalent stress must be less than (<) the tensile strength of the material of the pin divided by a safety factor.
In reality the problem has three dimensions. Depending on the suspensions of the vehicle and other structural features, additional momentums at the direction of x might be applied to the joints.
This is a rough static load calculation that needs verification. Additional dynamic calculations should be considered. Load calculations, for the case that the vehicle is decelerating or climbing down a slope, might also be necessary.