LifeTrac IV/Research Development/Carrying capacity
Overview
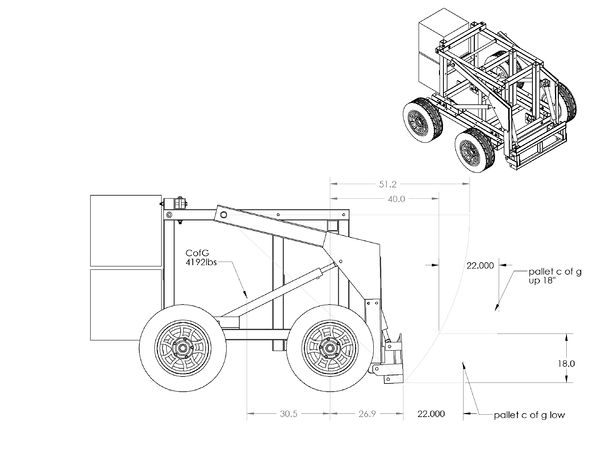
This page provides information for the approximate carrying capacity before vehicle tipping. Additional information is desired to determine structural strength when loaded. Operating load is defined as 50% of the tipping load.
C of G Analysis
- Mass is approximate to +/- 200lbs
- Tipping load is calculated by summing the moments around the front axle
Force Distribution Analysis
Wanted: Formulas for calculating the force distribution as a function of arm angle
- Assume symmetric along center plane
- LifeTrac image in MS Word file
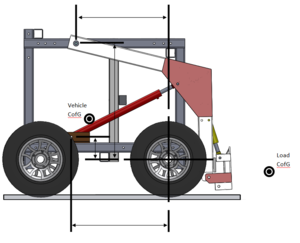
- Basically what we need is an understanding between carried load CofG, vehicle CofG, arm pivot location, hydraulic cylinder mounted location and the front wheel which acts as the point to tip around.
- Keep everything in x-y coordinate system for the initial static analysis and then provide the formula as a function of load location as it arcs around the loader arm pivot point at the top of the frame.
- The end goal is to have a formula that can be applied to any design
- Add whatever additional considerations are required to make the analysis more accurate
- Please provide definitions of variables used, easily understood diagram and formulas
- If uploading to wiki is a problem, please email data to Mike Apostol directly
Tipping load calculations
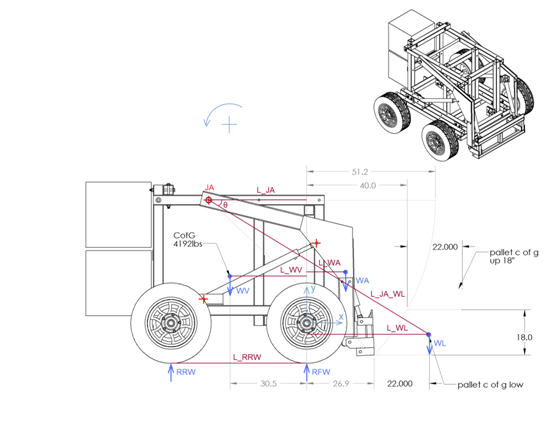
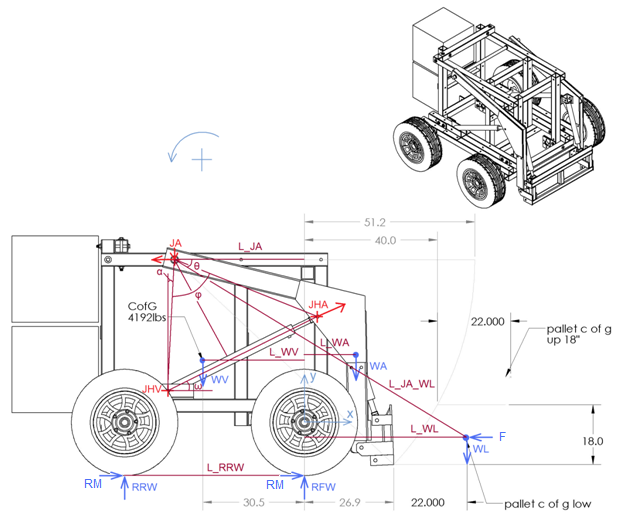
WL: Weight of load (pallet). All the weights are forces i.e. W=m*g.
WA: Weight of arm
WV: Weight of vehicle (without the weight of arm)
RFW: Reaction force at the front wheels
RRW: Reaction force at the rear wheels
L_WL: The distance between the c of g of the pallet (where WL is applied) and the vector y
y: The vertical vector that passes through the axis of the front wheels
JA: The position of the joints that support the arm on the frame of the vehicle
L_JA_WL: The distance between the joint of the arm and the c of g of the pallet
θ: The angle between the L_JA_WL and the horizontal
g: The gravity of Earth ( g = 9.81 m/(sec^2) )
Important: All the weights are forces. You can calculate them by multiplying the mass of each part by the gravity of Earth.
W = m*g , where if m is in [Kg] and g is in [m/(sec^2)], then W is in [N] (i.e. Newton). (1 lbs = 0.45359237 Kg)
RFW is the summation of the reaction forces applied to the two front wheels. I do not include the weight of the arm in the weight of the vehicle, because the position of the center of gravity of the arm changes while the arm rises. The same might be considered for the hydraulic cylinders, in more detailed calculations.
Balance of moments:
L_WV*WV – L_RRW*RRW – L_WL*WL – L_WA*WA = 0
where,
L_WL = L_JA_WL*cos(θ) – L_JA
Similar equation can be found for L_WA. Negative value of the L_WA implies that the c of g of the arm lies on the left side of the vector y.
The vehicle is tipping when RRW=0. Thus the tipping load is:
WL_tipping = (L_WV*WV – L_WA*WA)/L_WL
and the mass of the tipping load is: WL_tipping/g
For any WL, the reaction force on each wheel of the rear axis is the half of RRW, where:
RRW = (L_WV*WV – L_WL*WL – L_WA*WA)/L_RRW
The balance of forces implies that:
– RRW – RFW + WV + WL + WA = 0
Therefore, the reaction force on each wheel of the front axis is 0.5*RFW, where:
RFW = WV + WL + WA – RRW
Warning: Tipping load calculations, for the case that the vehicle is decelerating or climbing down a slope, might be also necessary.
Calculations of the static force on the joint of the arm
Warning: This is a rough static load calculation that needs verification. Additional dynamic calculations should be considered.
Case 1: tractor is used for lifting objects
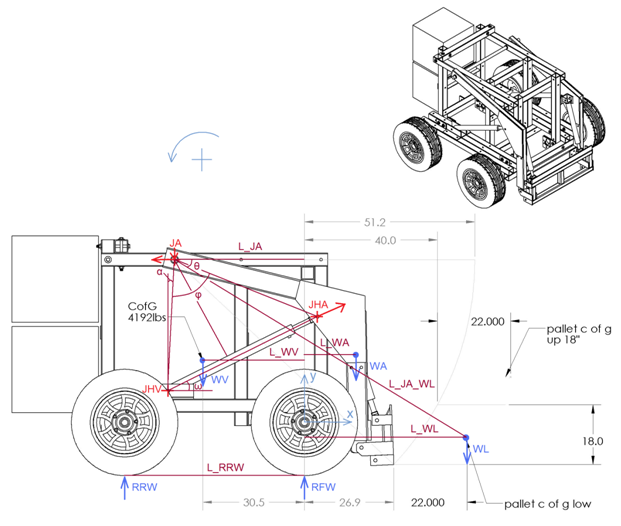
JA: The joint between the arm and the frame of the vehicle
JHV: The joint between the hydraulic cylinder and the frame of the vehicle
JHA: The joint between the hydraulic cylinder and the arm
R_JAy: The force applied from the vehicle to the arm, at vertical direction
R_JAx: The force applied from the vehicle to the arm, at horizontal direction
R_JHA: The force applied from the hydraulic cylinders to the arm
R_JHAy: The vertical component of the force applied from the hydraulic cylinders to the arm
R_JHAx: The horizontal component of the force applied from the hydraulic cylinders to the arm
ω: The angle between the direction of the hydraulic cylinder and the horizontal
L_JA_JHV: The distance between the positions of the joint JA and the joint JHV
L_JA_JHA: The distance between the positions of the joint JA and the joint JHA
L_JHV_JHA: The current length of the hydraulic cylinder (from joint JHV to joint JHA)
The force R_JHA is always in the direction of the axis of the hydraulic cylinder. That is because the joints of the cylinder cannot transmit moments at the direction of z.
(90deg – ω – α) is the angle between the L_JA_JHV and the L_JHV_JHA (i.e. the angle that has as a tip the joint JHV and as ends the joints JHA and JA).
sin(90deg – ω – α)/L_JA_JHA = sin(φ)/L_JHV_JHA =>
cos(ω+α)/L_JA_JHA = sin(φ)/L_JHV_JHA =>
cos(ω+α) = sin(φ)*L_JA_JHA/L_JHV_JHA =>
ω = arccos(sin(φ)*L_JA_JHA/L_JHV_JHA) – α
Balance of the moments applied at the arm (calculated at the position of JA):
L_JA_JHV* sin(90deg – ω – α)*R_JHA – (L_JA + L_WL)*WL – (L_JA + L_WA)*WA = 0 =>
L_JA_JHV*cos(ω+α)*R_JHA – (L_JA + L_WL)*WL – (L_JA + L_WA)*WA = 0
Thus, the force applied from the hydraulic cylinders to the arm is:
R_JHA = ( (L_JA + L_WL)*WL + (L_JA + L_WA)*WA )/( L_JA_JHV*cos(ω+α) )
The vehicle is symmetric, so each of the two cylinders applies a force to the arm that equals to 0.5*R_JHA.
The balance of forces at the vertical direction gives:
R_JAy = R_JHA*sin(ω) – WL – WA
The balance of forces at the horizontal direction gives:
R_JAx = R_JHA*cos(ω)
The total force R_JA is:
R_JA = ( (R_JAx)^2 + (R_JAy)^2 )^0.5
This force is distributed equivalently to the two joints between the arm and the frame of the vehicle. Thus, 0.5*R_JA is applied to each joint. If there is no bending on this cylindrical joint, the maximum shear stress is:
τ_shear = (4/3)*F/A
where F = 0.5*R_JA is the applied force and A = pi*r^2 is the cross-sectional area of the pin (that has radius r) of the joint. pi is 3.14.
The equivalent tensile stress is:
σ_total = 2*τ_shear
This equivalent stress must be less than (<) the tensile strength of the material of the pin divided by a safety factor.
Warning: In reality the problem has three dimensions. Depending on the suspensions of the vehicle and other structural features, additional moments at the direction of x might be applied to the joints.
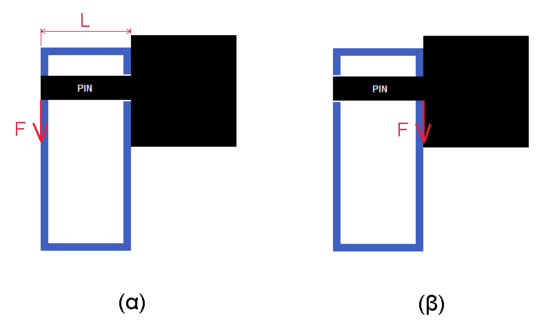
For instance, let’s assume that the holes of the tube where the pin fits are not identical (i.e. only one hole and the pin are in contact). At the pin of the joint that is illustrated in picture (β), only shear force is applied, and its stress (τ_shear) can be calculated as above. On the other hand, at the pin of the joint that is illustrated in picture (α) shear force and bending moment are applied. The stress from the shear force is calculated as above. The stress from the bending moment is:
σ_bending = (M/I)*r
where, M=F*L
is the applied moment at the pin, F is the force applied at the end of the pin and L is its length (distance from the start point of the pin to the point that F is applied).
I = (pi/4)*r^4
is the second moment of inertia of the cross section of the pin and r is its radius.
In this case, which both shear force and bending moment are applied, the equivalent tensile stress is calculated using the equation below.
σ_total = ( σ_bending^2 + 4 * τ_shear^2 )^0.5
Case 2: tractor is used for pushing objects
T_max: The maximum torque of the motor that is on each wheel.
r_wheel: The radius of the wheels.
F can be the reaction force that is applied when the tractor pushes the objects. At the picture above it is assumed that the contact point, which force F is applied, is close to pallet c of g. However, similar equations can be solved wherever the contact point is.
If each wheel has a driving motor then:
F = 4* T_max/r_wheel
Balance of the moments applied at the arm (calculated at the position of JA):
L_JA_JHV*cos(ω+α)*R_JHA – (L_ JA + L_ WL)*WL – (L_ JA + L_ WA)*WA – L_JA_WL*sin(θ)*F= 0
Thus, the force applied from the hydraulic cylinders to the arm is:
R_JHA = ( (L_ JA + L_ WL)*WL + (L_ JA + L_ WA)*WA + L_JA_WL*sin(θ)*F )/( L_JA_JHV*cos(ω+α) )
The vehicle is symmetric, so each of the two cylinders applies a force to the arm that equals to 0.5*R_JHA.
The balance of forces at the vertical direction gives:
R_JAy = R_JHA*sin(ω) – WL – WA
The balance of forces at the horizontal direction gives:
R_JAx = R_JHA*cos(ω) – F
The total force R_JA is:
R_JA = ( (R_JAx)^2 + (R_JAy)^2 )^0.5
This force is distributed equivalently to the two joints between the arm and the frame of the vehicle. Thus, 0.5*R_JA is applied to each joint.
Case 3: impact
Force F could also be considered as an impact force of several g (x in number). In this case F = x*g*(WV/g + WA/g).
Calculations of the forces on the bolts that mount the base of the hydraulic cylinders to the frame
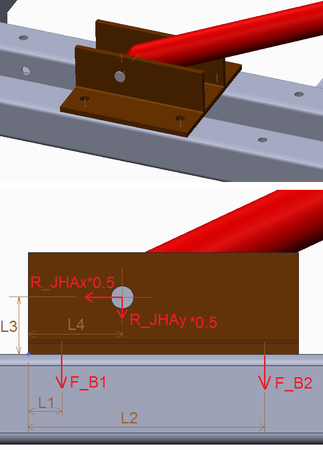
The picture below illustrates the base of each of the two hydraulic cylinders that raises the arm. Each of these two identical bases is mounted to the frame with four bolts. These four bolts are distributed in two rows.
Each bolt of the first row applies a force of 0.5*F_B1 to the plate.
Each bolt of the second row applies a force of 0.5*F_B2.
The hydraulic cylinder applies a force of 0.5*R_JHAx (at the horizontal direction) to the base and 0.5*R_JHAy at the vertical direction, because R_JHA is the force of the two hydraulic cylinders that we calculated earlier.
Balance of moments (at the point that is marked by the blue dot in the picture):
L3*0.5*R_JHAx – L1*F_B1 – L2*F_B2 – L4*0.5*R_JHAy = 0
Also, F_B1/L1 = F_B2/L2.
The second equation implies that F_B2 > F_B1 since L2 > L1, so we only need to calculate F_B2.
Proof: The second equation is derived by the following fact. The four bolts are the same and if we consider them as “springs” they will have the same spring constant k. If δ1 and δ2 are the elongations of the bolts of the first and second row respectively, then (0.5*F_B1)/δ1 = (0.5*F_B2)/δ2 = k. In addition δ1/L1 = δ2/L2 (similar triangles). Although that the elongations are very small, they imply that only the corner of the base is really in contact with the frame (blue dot in the picture). This is true when R_JHAx is far greater than R_JHAy (i.e. F_B2 is greater than zero, assuming that there is no pre-stress at bolts).
If we solve the above equations we find that:
L3*0.5*R_JHAx – (L1^2/L2)*F_B2 – L2*F_B2 – L4*0.5*R_JHAy = 0 =>
F_B2 = (L3*0.5*R_JHAx – L4*0.5*R_JHAy )/( (L1^2/L2) + L2 )
If F_B2 is negative, then there is not tensile force on the bolts and only the shear force is applied. The shear force of 0.5*R_JHAy is distributed equivalently on the four bolts. This means that (0.5*R_JHAy)/4 is applied on each bolt of the second row as a shear force. Thus, the shear stress is: τ_shear = (4/3)*( (0.5*R_JHAy)/4 )/A_B, where A_B is the cross section area of the bolt. The equivalent stress of the bolt is σ_total = 2 * τ_shear, in this case.
If F_B2 is positive, then a 0.5*F_B2 tensile force is applied on each bolt of the second row, in addition to the shear force. The tensile stress is: σ_tensile = (0.5*F_B2)/A_B. The shear stress is again τ_shear = (4/3)*( (0.5*R_JHAy)/4 )/A_B. The equivalent stress of the bolt is now σ_total = ( σ_tensile^2 + 4 * τ_shear^2 )^0.5.
Warning: If the bolt is pre-stressed, then σ_total is much greater.
A bolt is a sensitive mechanical element. A safety factor of 9 should be considered for it if its equivalent stress is compared with the ultimate tensile strength of its material (i.e. the stress where the material fractures). For a bolt of grade 8.8 the ultimate tensile strength is 830MPa (i.e. 830N/(mm^2) ).
Warning: We must always use a spring washer or a locknut or else the bolt might become loose.
The same method can be used to calculate the equivalent stress on every bolt of the vehicle.
Pre-stressed bolt
A bolt is pre-stressed when you tighten it more than it is needed to flatten the spring washer. You can use a torque-wrench to measure the torque Mt that you apply when you tighten the bolt. This torque usually remains after the tightening. The additional shear stress that is applied when tightening (because of Mt) is:
τ_shear_tighten = Mt/Wp
and it should be added to the load shear stress τ_shear, which is calculated above.
Wp = (pi*(d_b/2)^3 )/2
and d_b is the diameter of the bolt.
A tensile pre-stress also remains, when you tighten a bolt. This additional tensile stress is:
σ_tensile_tighten = E*δ_B/L_B
and it should be added to the load tensile stress σ_tensile that is calculated above.
E is the Young’s modulus of elasticity, L_B is the length of the bolt and δ_B is the pre-elongation of the bolt due to tightening (i.e. the increment of its length due to tightening). It is difficult to calculate δ_B. A rough approximation is δ_B = (angle_b/360deg)*pitch_length, where angle_b is the angle (in deg) that you revolve the bolt when you tighten it and pitch_length is the distance between the two adjacent peaks of the thread of the bolt. However, keep in mind that δ_B is usually less than that because other parts also deform (e.g. the rectangular tube that the base is tightened to it with bolts).
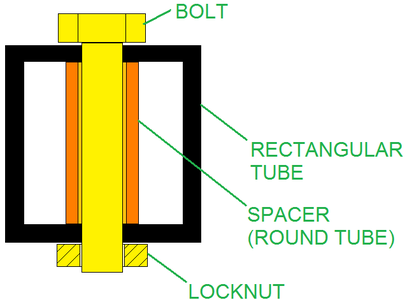
In order to avoid the deformation of the profile of the rectangular tube when you tighten the bolt, you can use a round tube, as a spacer inside the rectangular tube. This round tube supports the walls of the profile of the rectangular tube. The bolt passes through the round tube (see the picture below).
The conclusion is that you should be careful when tightening the bolt because additional permanent stresses are applied to it that might become really great in value. Over-tightening must be avoided.
Calculator for Stress Analysis of each module
File:Calculator for Stress Analysis of each module v0 1.xlsx
A few sets of calculations are written in the above excel workbook that concern some modules which can be used frequently in OSE machine designs. The idea is that since the machinery design is simple and uses standard parts (like beams and bolts), then analytical equations can be used to solve the stresses applied on each part. The goal is to avoid extreme oversizing of the components of the machines and therefore to reduce material and energy waste. The excel application is chosen for the calculations, since it can be found in almost every PC. The equations are also written as a text in the workbook, because it helps to an easier understanding and validation of the calculations and an easy copy/paste to other applications like scilab.
The V0.1 version of this excel workbook calculates:
- The stresses on the pin of a joint
- The forces on the mounting base of the hydraulic cylinder that is on lifetrac IV, as it is illustrated above
- The forces on the mounting base of the hydraulic cylinder that is on the backhoe
- The stresses on a bolt