Stepper Motor

From Open Source Ecology
(Redirected from Stepper Motors)
Jump to: navigation, search

Overview

Stepper Motor

A stepper motor (or step motor) is a brushless, electric motor that can divide a full rotation into a large number of steps. The motor's position can be controlled precisely without any feedback mechanism (see Open-loop controller), as long as the motor is carefully sized to the application.

How Stepper Motors Work

  • Basic animation on Wikipedia - 4 poles, multiple teeth - advance of 1/4 tooth per phase - so the resolution is number of teeth*number phases =25*4=100 in the example - [1]
  • See good overview. Note that steppers are typically made of 2-rotors of opposite polarity - [2]
  • Microstepping
  • Difference between 2 phase and 5 phase stepper motors - [3]
  • Comparison of stepper motor to brushless DC motor - [4]
  • Note that the combination of poles and phases determines the full step resolution. If you have many poles and 2 phases, you can advance in a number of steps proportional to the product of number of poles and number of phases. You can have many poles and 2 phases, or many poles and many phases - and each can give the same resolution. The ultimate resolution is determined by the number of poles and microstepping - where microstepping is activating the 2 rotors out of phase
  • https://www.motioncontroltips.com/faq-what-are-stepper-drives-and-how-do-they-work/

Holding Torque vs Moving Torque

  • 125 oz in hold for nema 17, example - [5]

More About How Steppers Work

Good description. Bottom line [6]:

  • Voltage of stepper is low, say 5V, but must be driven at 12-48V due to back emf
  • Inductance and resistance slow down the motor. The lower these quantities, the faster it can rotate.
  • A motor draws a constant current - control electronics work by limiting this current
  • If a motor draws 3A at 5V - what current does it draw when driven with 48V? Clearly it must be much lower or it would overheat from dissipated heat. [7] indicates that the drive is a chopper drive- ie, a switching power supply that handles power and probably at 20% energy loss.

Here is a second very useful response [8]:

  • Each phase takes the same power in a bipolar (2 phase) motor
  • What is the relationship of number of phases to number of windings?
  • What is the relationship between number of phases and number of wires?
  • Power dissipated by a stepper is I2R - and the actual current out of a power supply is simply P=IV. V_supply >> V_stepper, so current for a high power supply will be lower.

Here is information about full vs microstepping - full has 8-10% more torque than microstepping. [9]. If that is true for high speed - then we may want to consider full stepping to get 10% more power. Then the step resolution with our current system goes down to 160 microns from 10 microns (currently we use 16 microstepping). That is still perfectly fine for very large prints.

Voltage

Running steppers at higher voltage produces more torque. 20x rated voltage is ok. [10]

Power

See Minebea_Stepper_Motor_Specs#Power for insights about power use.

Lifetime

The typical lifetime for a stepper motor is 10,000 operating hours. This approximates to 4.8 years; given the stepper motor operates one eight-hour shift per day. The lifetime of a stepper motor may vary in regards to user application and how rigorous the stepper motor is run.[11]

See Also

Torque Tests

Test 1

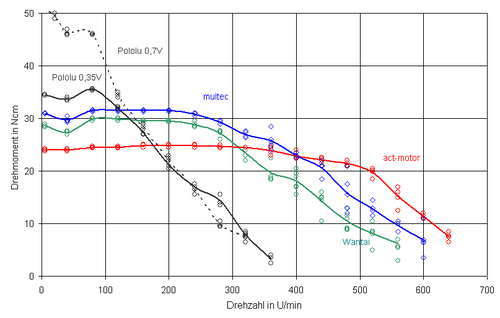
This test used Nema17 stepper motors driven by A4988 driver boards http://reprap.org/wiki/Stepper_torque

M vs n.PNG

Summary: All motors perform well at speeds < 100 revs/min. Dynamical torque starts to drop off at speeds higher than 300 rev/min. The higher the rated current and the lower the inductance, the better the performance at high speeds.

inside a stepper motor

Types of Stepper Motors

  • 17PM-K402 - Hybrid 2 and 4 phase - 6 volts rated - [13] - RAMPS wouldn't run it.
  • 12 V rated - [14] - RAMPS wouldn't run it

Sourcing

NEMA 34

  • $60 - 55 in lb - including driver and power supply - [15]
  • $50 - 77in lb - [16]
  • Geared - 354 in lb - 0.6" shaft, 6x planetary gear - $84 - [17]
  • 75 in lb - $77 - Ebay - [18]. 6A current.

NEMA 23

Nema 23 Stepper Motor

  • $33 - 425 oz in - [19]
  • $37 - 425 oz in, 3Nm, 27 lb - [20]. This would work with a 1" pulley, so drive radius is 1/2"
  • $40 - 425 oz in, 3Nm - [21]
  • $30 for 1.9Nm - [22]

Driver

  • 5A TB6600 driver - $14 each - [23]
  • 4A TB6600 driver is typically $8 - [24]

Small

  • 3A - $6 each - [25]
  • 4A - $9 each for 5 - [26]
  • 4A - Single - $11 - [27]

By Origin

Links

Retrieved from "https://wiki.opensourceecology.org/index.php?title=Stepper_Motor&oldid=192828"